Descargar este artículo  en Formato PDF:

 

 

 

 

 

 

 

 

 

Revista Científica UDO Agrícola Volumen 9. Número 4. Año 2009. Páginas: 912-924

 

Variabilidad espacial de las propiedades físicas de dos suelos cultivados con palma aceitera en el estado Monagas, Venezuela

 

Spatial variability of physical properties of two soils cultivated with oil palm in Monagas state, Venezuela

 

Renny BARRIOS MAESTRE  ¹ y Adriana FLORENTINO DE ANDREU ²

 

¹Instituto Nacional de Investigaciones Agrícolas (INIA). San Agustín de La Pica, Vía Laguna Grande. Apartado Postal 184. Maturín, estado Monagas Venezuela y ²Universidad Central de Venezuela. Facultad de Agronomía. Vía El Limón. Maracay, estado Aragua, Venezuela. E-mail: rbarrios@inia.gov.ve 

  Autor para correspondencia

 

 

RESUMEN

 

La variabilidad espacial de las propiedades físicas del suelo dentro de los campos agrícolas es consecuencia de los procesos de formación de suelo o puede ser inducida por prácticas de manejo del cultivo. Dada la necesidad de entender su comportamiento e interrelaciones y el impacto del manejo agronómico, el presente trabajo tuvo como objetivo evaluar la variabilidad de las propiedades físicas de dos suelos irrigados representativos de las plantaciones comerciales de palma aceitera del estado Monagas, a fin de cuantificar la distribución espacial del impacto que tiene el manejo agronómico del cultivo sobre el suelo. Para el muestreo se trazaron cinco transectas y se seleccionaron 102 puntos en el Ultisol y 92 puntos en el Vertisol. En los estratos 0-25, 25-50, 50-75 y 75-100 cm se evaluaron las varibles: conductividad hidráulica saturada (Ks), densidad aparente (Da), distribución de tamaño de partículas, porosidad total y macroporosidad. Se realizó un análisis exploratorio y un análisis geoestadístico. Se determinaron semivariogramas experimentales y se le ajustaron modelos teóricos. Se realizó la interpolación de Ks de 0-100 cm para estimar el impacto local del manejo de la plantación. La estadística clásica y los métodos geoestadísticos revelaron diferencias estadísticas y variabilidad espacial entre los suelos, entre los horizontes evaluados y a través del campo. La estructura de los semivariogramas experimentales reveló el impacto de la actividad antrópica sobre las propiedades físicas del suelo. La varianza estructurada fue dominante sobre el componente aleatorio del semivariograma. Los modelos teóricos ajustados fueron del tipo esférico y exponencial. Los mapas de contorno obtenidos por interpolación por ‘Kriging’ tienen gran potencialidad para diseñar estrategias de manejo por sitio específico.

 

Palabras clave: Elaeis guineensis, semivariograma, kriging, geoestadística, manejo por sitio específico.

 

ABSTRACT

 

The spatial variability of soil physical properties within the agricultural fields is a result of soil formation process or may be induced by crop management practices. Given the need to understand their behavior and interactions and the impact of agricultural practices, this study aimed to evaluate the variability of the physical properties of irrigated soils representing two commercial plantations of oil palm (Elaeis guineensis Jacq.) in Monagas. For the sampling five transects were drawn and 102 points were selected in the Ultisol and 92 points were selected in the Vertisol. In strata 0-25, 25-50, 50-75 and 75-100 cm were evaluated following variables: saturated hydraulic conductivity (Ks), bulk density (Da), particle size distribution, total porosity and macroporosity. Exploratory and geostatistical analysis were performed. Experimental semivariograms were determined and was adjusted theoretical models. Interpolation of Ks 0-100 cm was performed to estimate the impact of local management of the plantation. Classical statistics and geostatistical methods showed statistically significant differences and spatial variability between the soil,  between evaluated horizons and across the field. The structure of the experimental semivariograms revealed the impact of human activity on soil physical properties. The variance structure was dominant over the random component of the semivariograms. Spherical and exponential theoretical models were adjusted. Contour maps obtained by interpolation by 'Kriging' have great potential for designing strategies for site-specific management.

 

Key words: Elaeis guineensis, Semivariograms, kriging, geostatistical, site-specific management.

 

INTRODUCCIÓN

 

La utilización de los sistemas de información geográfica (SIG) en diversos campos del quehacer humano, se ha incrementado en los últimos años demostrando ser una herramienta muy útil en la toma de decisiones. En la agricultura tiene gran aplicabilidad en el área de contaminación de suelos, fertilidad y manejo de suelos, entre otras. Uno de los aspectos de mayor utilidad es el estudio de la variabilidad espacial de suelos y la predicción de valores en puntos no muestreados a través del uso de las interpolaciones (Henríquez et al., 2005).

 

La variabilidad espacial de las propiedades físicas del suelo dentro de los campos agrícolas es inherente a la naturaleza geológica de la formación de suelo, pero en algunos casos la variabilidad puede ser inducida por la labranza y otras prácticas de manejo. Estos factores interactúan unos con otros a través de escalas espaciales y temporales, y se modificarán una vez más a nivel local por los procesos de erosión y deposición (Iqbal et al., 2005)

 

Los aspectos más estudiados han sido las variaciones intrínsecas del suelo causadas por el material parental, como es el caso de cambios litológicos a través de un área determinada. La otra fuente de variación es la provocada por cambios que ocurren en el tiempo y que son provocados en gran medida por el manejo debido al tipo de uso del suelo (Bertsch et al., 2002).

 

Lo anterior ha permitido la implementación del concepto de manejo por sitio específico, apoyado en el uso de mapas cloropléticos, los cuales modelan dicha variación en forma de un conjunto de cuerpos geográficos discretos que se separan entre sí por discontinuidades o límites (Jenkins et al., 2000; Obando et al., 2006; Jaramillo, 2006; Ramírez-López et al., 2008).

 

La agricultura de precisión o de manejo de sitio-específico tiene por objeto la gestión de la variabilidad espacial del suelo mediante la aplicación de insumos de acuerdo con el sitio, los requisitos específicos de un determinado suelo y cultivo. Tales prácticas de manejo requieren la cuantificación de la variabilidad espacial del suelo en todo el campo (Mzuku et. al., 2005).

 

El tratamiento estadístico puro del problema de heterogeneidad ignora la existencia de correlación espacial, mientras que un análisis geoestadístico de la heterogeneidad calcula correlaciones entre las observaciones hechas en diferentes sitios vecinos. La correlación observada puede ser usada en aplicaciones prácticas tales como estimación de valores de las propiedades seleccionadas en localizaciones no muestreadas por medio de ‘kriging’ (Webster y Burgess, 1980) o técnicas de ‘co-kriging’ (Vauclin et al., 1983) o pueden ser usadas en el diseño de redes de muestreo (Mallants et al., 1996).

 

Se han realizado varios trabajos sobre la predicción espacial de propiedades del suelo a través del uso de un método geoestadístico conocido con el nombre de ‘kriging’, el cual considera la correlación entre muestras tomadas en sitios adyacentes para estimar el valor interpolado entre ellas con la mínima varianza, lo que ha generado su reconocimiento como el mejor estimador lineal insesgado.

 

La aplicación de este método requiere de tres asunciones básicas que conciernen a las propiedades estadísticas de los datos (Matheron, 1970):

 

1.    Los datos deben estar distribuidos normalmente o ser transformables a una distribución normal.

 

2.    Los datos deben poseer estacionaridad de segundo orden, lo cual puede ser expresado como:

 

E[Z_(x)-Z_(x+h)]=0

 

[Z_(x)-Z_(x+h)]²}=2g_(h)

 

Donde:

 

E(z): es el valor esperado de z

 

z(x): es una función aleatoria para la propiedad del suelo Z

 

h: es la distancia de separación entre dos lugares cualquiera x y x+h  y

 

g: es la semivarianza.

 

3.    Las variables deben ser aditivas, es decir, todas las combinaciones lineales de los valores de z deben conservar el mismo sentido.

 

Journel y Huijbregts (1978) indican que hay dos tipos de estacionaridad de los datos: la estacionaridad de segundo orden y la hipótesis intrínseca. La estacionaridad de segundo orden contempla lo siguiente:

 

1.        E[Z(x)]=m para cualquier x, lo cual implica que el valor esperado para una función aleatoria en el espacio existe y no depende de la localización x.

 

2.        E{[Z(x+h) - m] [Z(x) - m] = s(h) para cualquier x y h, lo que implica que para cada par de variables [Z(x+h) , Z(x)] la covarianza existe y depende solamente del vector de separación h.

 

Para el caso de la hipótesis intrínseca, los datos utilizados para el cálculo de la semivarianza requieren:

 

1.        E[Z(x)] = m para cualquier x, lo cual implica que el valor esperado para una función aleatoria en el espacio existe y no depende de la localización x.

 

2.        g(h) = 1/2{[Z(x+h) -  Z(x)]²} para cualquier h y x, lo cual define el valor de semivarianza e implica que las varianzas de las diferencias depende solamente de la separación del vector h.

 

En función de estas acotaciones, la función de semivarianza puede ser expresada por medio de la siguiente ecuación (Goovaerts, 1997):

 

g(h) = ½_N S{[Z(x+h) -  Z(x)]²}

 

Donde:

 

g(h): es la semivarianza

 

N: es el número de pares

 

Z(x): es el valor de la propiedad en el lugar x

 

Z(x+h): es el valor de la propiedad a una distancia h del lugar x.

 

El gráfico que relaciona la semivarianza con la distancia de muestreo se conoce como semivariograma. Generalmente la semivarianza aumenta con los incrementos de la distancia hasta alcanzar un valor estable denominado meseta o ‘sill’, la distancia a la cual se alcanza el umbral se denomina amplitud, alcance o rango y constituye la distancia hasta donde existe dependencia espacial entre las observaciones. Teóricamente, la semivarianza debería ser cero cuando la distancia es cero, esto realmente ocurre muy raras veces, manifestándose el efecto aleatorio de la varianza o efecto ‘pepita’, que es consecuencia de un tipo de variación imposible de detectar a la escala de muestreo o que puede evidenciar imprecisiones en los métodos utilizados para las evaluaciones.

 

En la determinación de los parámetros y componentes del semivariograma, el comportamiento de la semivarianza tiende a ser ajustado a modelos teóricos en forma visual (Journel y Huijbregts, 1978) o a través del procedimiento de los mínimos cuadrados, el cual se considera de alta precisión (Burrough, 1993). Los modelos más comúnmente usados en el ajuste de los semivariogramas son el lineal, esférico, exponencial, logarítmico y gaussiano (Webster y Oliver, 1990). La precisión de una estimación de ‘kriging’ está afectada por el semivariograma y por el número de observaciones utilizado. El semivariograma define la estructura de autocorrelación espacial de la variable y se usa para minimizar la desviación estándar de la estimación, mientras que el número de datos determina la precisión del variograma, ya que ésta decrece en la medida en que el conjunto de datos es menor.

 

El error estándar obtenido por ‘kriging’ es mucho menor que el calculado por medio de la estadística clásica; sin embargo, la varianza depende solamente del variograma y de la configuración de los puntos de muestreo en relación al punto o bloque a ser estimado, pero no depende de los valores observados. Por lo tanto, es necesario que el semivariograma teórico presente buen ajuste de manera que refleje la variabilidad real presente en la zona (Bregt et al., 1991). Dada la importancia del manejo de las propiedades del suelo en la producción agrícola, así como la necesidad de entender el comportamiento, la relación de estas y el impacto del hombre sobre el agroecosistema, el trabajo tuvo como objetivo evaluar la variabilidad de las propiedades físicas de dos suelos irrigados representativos de las plantaciones comerciales de palma aceitera del estado Monagas, a fin de cuantificar la distribución espacial del impacto que tiene el manejo agronómico del cultivo sobre el suelo.

 

MATERIALES Y MÉTODOS

 

Ubicación

 

La evaluación se condujo en las plantaciones comerciales de palma aceitera de la empresa Palmas de Monagas C.A. (PALMONAGAS, C.A.), ubicadas en el Asentamiento Campesino “El Zamuro”, municipio autónomo Maturín del Edo. Monagas, ubicada en las coordenadas  9° 53’ 08’’ LN y 63° 05’ 36’’ LO, y está enmarcado dentro del Convenio de Cooperación Técnica firmado entre el FONAIAP (CIAE Monagas), FONINPAL y PALMONAGAS C.A.

 

Clima

 

Está clasificado como Bosque Húmedo Tropical. En esta zona la temperatura media anual es de 27,3^o C, la precipitación es del orden de 1291 mm como promedio anual; la humedad relativa es superior al 80% durante todo el año y la altitud se encuentra entre los  30 y 40 m.s.n.m.

 

Suelos

 

Los suelos donde se llevó a cabo el ensayo fueron seleccionados ya que son representativos de las plantaciones comerciales del Estado Monagas, están ubicados dentro del paisaje de terrazas aluviales del río Punceres y tienen una pendiente inferior al 1%. Uno de los suelos se clasifica como Typic Plinthudults (Francosa fina, mixta, isohipertérmica), con un estrato plintítico de profundidad variable (0,8 a 1,6 m), de baja fertilidad y comprendidos dentro del área geomorfológica terraza media plana. El otro suelo fue clasificado como Entic Pelluderts (Arcillosa fina, mixta, isohipertérmica) con un estrato de plintita a partir de 1,6 m de profundidad y de drenaje lento ubicado en la vega del río Punceres (Pérez, 1987)

 

Esquema de Muestreo

 

Para efectuar el muestreo se trazaron cinco transeptos de 125 m cada una, paralelas entre sí, con una separación de 22,5 m donde se realizaron muestreos a intervalos de distancia que variaron entre 2 y 12 m, lo cual generó un total de 102 puntos para el caso del Ultisol y 92 puntos de muestreo para el caso del Vertisol.

 

En cada punto de muestreo se evaluaron las siguientes variables:

 

1.      Conductividad hidráulica saturada

 

Se  utilizó el método del pozo barrenado invertido o método de Porchet (Razuri, 1978) para realizar pruebas de conductividad hidráulica, alrededor de cada punto de muestreo, en cuatro profundidades diferentes: desde la superficie hasta 25 cm; desde la superficie hasta 50 cm;  desde la superficie hasta la profundidad del estrato plintítico y desde la superficie hasta 100 cm para el Ultisol; en el caso del Vertisol se consideraron las profundidades: 0 a 25 cm,  0 a 50 cm, 0 a 75 cm y 0 a 100 cm.

 

2.      Densidad aparente

 

            Se evaluó por medio de la obtención de muestras inalteradas a través del barreno tipo Uhland, con cilindros de aproximadamente 100 cm³ de volumen, procediéndose luego a la determinación del peso seco de la muestra mediante el secado en estufa a una temperatura de 105^o C, según metodología descrita por Blake y Hartge (1965). Las evaluaciones se efectuaron a las profundidades de 0 a 25 cm; de 25 a 50 cm; de 50 a 75 cm y de 75 a 100 cm.

 

3.      Porosidad

 

            Las muestras inalteradas de suelo colectadas se saturaron con agua para obtener el espacio poroso total, y luego se procedió a la discriminación de poros con diámetro mayor a 30 mm  (macroporosidad) a través de la aplicación de una succión de 100 cm (10 kPa) en la mesa de tensión aplicando el método descrito por Pla (1983).

 

4.      Distribución de tamaño de partículas

 

            La evaluación se realizó a través del método de Bouyoucus modificado (Day, 1965) en sólo el 50% de los puntos de muestreo, analizándose puntos ubicados a distancias de 10 m en las transeptos.

 

Tratamiento estadístico

 

El tratamiento estadístico aplicado a las variables relacionadas con las propiedades hidráulicas de los suelos estudiados fue:

 

Análisis exploratorio

 

Los resultados obtenidos fueron sometidos a un análisis exploratorio con el fin de detectar los valores atípicos que puedan afectar la calidad del resto de los análisis estadísticos. Dicho análisis se realizó a través del programa GeoEAS (Englund y Sparks, 1988) y se definieron los estadísticos básicos: media, mediana, coeficiente de variación, asimetría y curtosis.  Con el programa PROGRESSA (Silva-Acuña et al., 1995) se determinó si los datos presentaban una distribución normal. La eliminación de datos atípicos se realizó siguiendo la metodología descrita por Tukey (1977).

 

Los datos obtenidos se sometieron a una comparación con la distribución normal por medio de la Prueba de Normalidad de Lilliefors a un nivel de probabilidad de 5%. En aquellos casos donde se rechazó la hipótesis de la distribución normal se procedió a efectuar transformaciones según las recomendaciones realizadas por Webster y Oliver (1990) con el propósito de lograr que la distribución de los datos se asemeje a la normal.

 

Análisis geoestadístico

 

Debido a que la forma exacta del modelo del semivariograma no se conoce con antecedencia, los modelos seleccionados y usados solo fueron una aproximación de su función (Journel and Huijbregts, 1978). Por lo tanto, cada semivariograma para cada variable de suelo se ajustó por ensayo y error hasta que se encontró el mejor ajuste entre los valores estimados y los valores reales (Bailey and Gatrell, 1995).

 

El análisis geoestadístico se realizó a través del programa Variowin (Pannatier, 1994). Se calculó un semivariograma para cada variable para determinar el grado de variabilidad espacial entre observaciones vecinas, y se ajustó la función modelo apropiada al semivariograma, haciéndose énfasis en los semivariogramas direccionales debido al interés en evaluar el comportamiento de los atributos del suelo en el sentido perpendicular a los canales secundarios de riego (sentido este-oeste).

 

A partir de los semivariogramas experimentales ajustados se obtuvieron los distintos parámetros del modelo de variación: rango, varianza aleatoria (Efecto Pepita) y varianza total (meseta). Una vez obtenidos los parámetros del modelo de variación de los suelos, se procedió a clasificar el grado de dependencia espacial de las variables evaluadas según los señalamientos realizados por Cambardella et al. (1994) quienes, a través de la relación entre la varianza aleatoria y la varianza total expresada en porcentaje, destacan que una proporción menor de 25% indica una fuerte dependencia espacial; entre 25% y 75% indica una moderada dependencia espacial y mayor a 75% es reflejo de una dependencia espacial débil.

 

El objetivo final del análisis geoestadístico es la estimación de los atributos del suelo en lugares no evaluados por medio de la interpolación. El método más usado para efectuar dicha interpolación es ‘kriging’ puntual (Trangmar et al., 1985), para lo cual es conveniente que los datos se distribuyan normalmente y cumplan con los supuestos de la hipótesis intrínseca (Hamlett et al., 1986; Burrough, 1993). Cuando no se cumplen los requerimientos de la hipótesis intrínseca requeridos por ‘kriging’ puntual, se recomienda el uso de distintas metodologías de ‘kriging’, tales como universal o disyuntivo (Trangmar et al., 1985), sin embargo, diversos estudios demuestran que el ‘kriging’ ordinario es lo suficientemente robusto como para tolerar cierto grado de no estacionaridad de los datos.

 

En función de lo anterior, para cada suelo se seleccionó la variable “conductividad hidráulica saturada” (Ks) a la profundidad de 0 a 100 cm, como una variable integradora y de gran importancia en el manejo del cultivo, a fin de efectuar las interpolaciones por medio de ‘kriging’ puntual y para analizar los resultados en función de las condiciones de manejo de la plantación.

 

RESULTADOS Y DISCUSIÓN

 

Análisis Exploratorio

 

Presencia de valores atípicos

 

A través del análisis exploratorio se determinaron los estadísticos básicos para las variables densidad aparente (Da), porosidad total (PT), macroporosidad (Mp), arcilla, limo y arena en los diferentes estratos de los suelos estudiados en el presente trabajo, cuyos resultados aparecen en los cuadros 1 y 2 para el Ultisol y el Vertisol, respectivamente. Este análisis también permitió determinar la presencia de valores muy lejanos (Tukey, 1977) y comprobar el ajuste de la distribución de frecuencia de los datos a la curva de distribución normal, a través de los estadísticos ‘asimetría’ y ‘curtosis’ del programa GeoEAS (Englund y Sparks, 1988) y de la prueba de normalidad de Lilliefors del programa PROGRESSA (Silva-Acuña et al., 1995).

 

 

 

 

 

Cuadro 1. Estadísticos para las variables evaluadas en un Ultisol irrigado cultivado con palma aceitera en el estado Monagas, Venezuela.
Profundidad (cm)	Variable	Media	Mediana	Coef. de Variación	Asimetría	Curtosis	F Calculada
0-25	Da (Mg.m-3)	1,54	1,55	5,22	-0,61	3,46	0,066*
	PT (%)	33,4	33,4	8,63	-0,12	3,07	0,042*
	Mp (%)	9,40	8,98	29,0	0,28	3,02	0,074*
	Arcilla (%)	12,68	12,70	27,7	0,72	3,23	0,981*
	Limo (%)	25,49	25,40	9,76	0,32	2,40	0,950*
	Arena (%)	61,83	62,80	7,27	-0,53	2,50	0,118*
25-50	Da (Mg.m-3)	1,59	1,59	4,04	0,73	4,23	0,113 ns
	PT (%)	32,0	31,8	9,77	0,12	2,66	0,048*
	Mp (%)	7,93	7,95	33,5	0,26	2,33	0,087*
	Arcilla (%)	16,67	16,00	22,66	0,67	3,50	0,113*
	Limo (%)	23,98	23,10	18,84	0,81	3,49	0,142 ns
	Arena (%)	59,35	60,60	9,24	-0,79	3,61	0,136 ns
50-Plintita	Da (Mg.m-3)	1,59	1,60	3,50	0,14	3,39	0,083*
	PT (%)	33,4	33,1	11,2	0,52	3,74	0,057*
	Mp (%)	7,37	7,42	36,8	0,15	2,98	0,063*
	Arcilla (%)	23,79	21,00	34,75	0,57	2,35	0,165*
	Limo (%)	22,62	22,80	19,82	-0,05	2,51	0,065*
	Arena (%)	53,59	56,00	16,72	-0,63	2,76	0,102*
Plintita-100	Da (Mg.m-3)	1,58	1,58	4,60	0,12	4,60	0,086*
	PT (%)	36,1	36,1	12,4	-0,23	2,73	0,040*
	Mp (%)	6,35	6,54	37,3	-0,02	3,06	0,046*
	Arcilla (%)	29,54	30,95	24,49	-1,07	3,91	0,137 ns
	Limo (%)	19,29	18,7	21,46	0,78	3,89	0,125ns
	Arena (%)	51,17	51,05	12,96	0,41	2,71	0,110*
Da = Densidad aparente; PT = Porosidad total; Mp = Macroporosidad  * = Significativo a P≤ 5%, ns = no significativo

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cuadro 2. Estadísticos  para  las  variables  evaluadas  en un Vertisol irrigado cultivado con palma aceitera en el estado Monagas,  Venezuela.
Profundidad (cm)	Variable	Media	Mediana	Coef. de Variación	Asimetría	Curtosis	F Calculada
0-25	Da (Mg.m-3)	1,35	1,35	7,14	0,27	2,16	0,087 *
	PT (%)	44,7	45,2	10,7	0,41	3,94	0,091 *
	Mp (%)	5,12	5,02	49,0	0,71	3,54	0,107 ns
	Arcilla (%)	43,55	43,40	17,57	0,067	2,00	0,088 *
	Limo (%)	23,91	24,40	19,82	-0,67	2,21	0,097 *
	Arena (%)	32,54	31,10	7,14	0,54	2,30	0,087 *
25-50	Da (Mg.m-3)	1,40	1,39	7,05	-0,19	2,80	0,053 *
	PT (%)	43,2	44,0	9,94	-0,59	3,46	0,088 *
	Mp (%)	4,22	4,27	49,6	0,29	2,51	0,059 *
	Arcilla (%)	42,48	42,05	20,33	-0,42	3,09	0,067 *
	Limo (%)	22,90	22,19	18,89	0,71	2,62	0,123 *
	Arena (%)	34,62	31,55	24,50	0,64	2,58	0,157 ns
50-Plintita	Da (Mg.m-3)	1,44	1,46	7,65	-0,27	1,90	0,098 ns
	PT (%)	42,2	42,1	11,5	-0,12	2,59	0,038 *
	Mp (%)	3,16	3,15	54,4	0,33	2,42	0,083 *
	Arcilla (%)	43,97	45,70	26,29	-0,42	2,18	0,099 *
	Limo (%)	20,74	20,75	15,69	0,24	2,83	0,064 *
	Arena (%)	35,29	30,65	31,25	0,82	2,68	0,220 ns
Plintita-100	Da (Mg.m-3)	1,49	1,50	7,64	-0,43	2,68	0,079 *
	PT (%)	40,5	40,2	12,7	-0,02	2,50	0,091 *
	Mp (%)	3,62	3,22	65,3	0,98	3,82	0,103 ns
	Arcilla (%)	41,54	41,55	30,33	-0,08	2,21	0,105 *
	Limo (%)	20,50	20,90	14,72	-0,43	3,36	0,061 *
	Arena (%)	37,97	34,65	31,35	0,39	2,23	0,129 ns
Da = Densidad aparente; PT = Porosidad total; Mp = Macroporosidad  * = Significativo a P≤ 5%, ns = no significativo

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En el caso del Ultisol (Cuadro 1), las variables: porosidad total a las profundidades de 25 a 50 cm y de 50 a 75 cm; macroporosidad a partir de los 25 cm de profundidad y la variable densidad aparente a partir de los 50 cm, presentaron valores muy lejanos, los cuales fueron removidos para proceder a la ejecución e interpretación del análisis exploratorio y de otros análisis subsiguientes. De la misma manera se procedió con el Vertisol (Cuadro 2), donde solamente las variables densidad aparente a la profundidad de 0 a 25 cm y la porosidad total a la profundidad de 25 a 50 cm presentaron valores muy lejanos.

 

En el Ultisol se observó que la Da presentó un valor medio de 1,54 Mg.m^-3en el estrato de 0 a 25 cm, valor que aumentó a 1,59 Mg.m^-3 a partir de los 25 cm y luego se mantuvo prácticamente constante; la PT se mantuvo prácticamente constante a través del perfil, mientras que la Mp disminuyó de 9,4% en la superficie a 6,5% entre 75 y 100 cm de profundidad; sin embargo, es importante destacar que a partir de los 25 cm existe un incremento en el contenido de arcilla (pasando de 12,7% en el estrato superficial a 29,5% entre 75 y 100 cm) y una reducción en el contenido de arena. Esta situación debería reflejarse en una disminución de los valores de Da y en incrementos en la PT según los hallazgos de Ahuja et al. (1985), Horn et al. (1995) y Barrios y Florentino (2008).

 

El comportamiento de las variables en el Vertisol mostró algunas similitudes con el Ultisol, ya que se obtuvo incremento en los valores de Da a través del perfil, la cual varió desde 1,35 Mg.m^-3 en la superficie a 1,49 Mg.m^-3a los 75 cm de profundidad; la Pt disminuyó de 44,7% a 40,5% y la Mp de 5,1% a 3,1%.

 

En líneas generales, en ambos suelos el estrato superficial mostró valores normales de acuerdo a su clase textural (Florentino, 1996), pero revela la presencia de horizontes compactados a partir de los 25 cm de profundidad, tal como fue reportado por Barrios y Florentino (2008) para los suelos palmeros del estado Monagas, atribuidos al uso de maquinaria agrícola durante el proceso de deforestación, apilamiento de los troncos y extracción de las raíces del suelo; control de malezas con rotativas en etapas jóvenes del cultivo y el paso de carretas y animales de tiro para la cosecha en plantaciones adultas (Dufour y Olivin, 1985; Caliman et al., 1987; 1990).

 

En cuanto a la variabilidad, medida en términos del coeficiente de variación, se encontró que para ambos suelos y para todos los estratos, la variable Macroporosidad (Mp) fue la que presentó los mayores coeficientes de variación. En esta variabilidad se incluye la que ocurre en forma natural, debido a las variaciones que incorpora el horizonte argílico en el Ultisol y los procesos de apertura y cierre de grietas que se produce en el Vertisol; por otro lado, se refleja la incidencia del problema de compactación mencionado anteriormente.

 

Análisis Geoestadístico

 

Los semivariogramas experimentales para las variables analizadas, tanto para el Ultisol como para el Vertisol, presentaron incrementos de la semivarianza con la distancia hasta estabilizarse, indicando la presencia de dependencia espacial. La Figura 1 muestra el comportamiento de la variabilidad espacial, a través de semivariogramas experimentales, para dos variables de cada uno de los suelos estudiados. Estos semivariogramas reflejan la participación de al menos tres fuentes de variación que contribuyen a la variabilidad espacial: la varianza aleatoria, atribuida a la variabilidad ocurrida a distancias menores a las de muestreo; la varianza total (variabilidad intrínseca), atribuida a la variabilidad natural del suelo, y una fuente de variación antrópica (variabilidad extrínseca) que se refleja en un comportamiento irregular del semivariograma, y que ocurre entre la varianza aleatoria y la varianza total.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

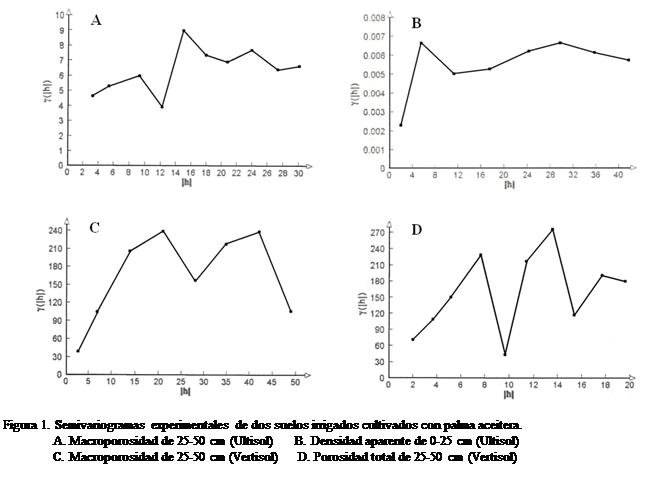
En tal sentido, las Figuras 1A y 1D, correspondientes a la macroporosidad entre 25 y 50 cm en el Ultisol, y a la porosidad total a la misma profundidad en el Vertisol, respectivamente, presentan un incremento de la semivarianza con la distancia, el cual se ve interrumpido por un descenso brusco entre los 10 y 14 m, distancia que se aproxima a la distancia de separación que existe entre las interlíneas de circulación de los vehículos utilizados para la cosecha. Este  comportamiento indica que existe una tendencia hacia la homogeneización de las propiedades del suelo en el área de circulación.

 

En el caso del Vertisol, la variable macroporosidad entre 25 y 50 cm (Figura 1C) muestra un comportamiento diferente, ya que el descenso de la semivarianza ocurre a los 30 m aproximadamente, lo cual corresponde a la distancia de separación de los canales de  riego. Por su parte, la densidad aparente de 0 a 25 cm en el Ultisol (Figura 1B) presenta un incremento marcado de la semivarianza entre 5 y 9 m, rango dentro del cual se ubica la distancia de separación de las hileras de siembra, y donde se alinea gran parte de la materia orgánica proveniente de la poda de las palmas.

 

Existe un comportamiento bien diferenciado en la semivarianza de las propiedades del suelo, dependiendo de la posición que ocupen dentro de la plantación. Los semivariogramas experimentales reflejan que la actividad antrópica es una fuente importante en la alteración de la estructura natural de variación de las propiedades del suelo, fenómeno que está asociado con el problema de compactación descrito anteriormente. Aparentemente, la formación de horizontes compactados tiende a homogeneizar las propiedades del suelo, mientras que los sitios poco afectados por fuerzas mecánicas externas y con aportes de materia orgánica tienden a ser mucho más variables.

 

Varios autores también han reportado un comportamiento diferencial de los horizontes compactados, bien sea en plantaciones jóvenes (Caliman et al., 1990), en plantaciones adultas (Peralta et al., 1985; Dufour y Olivin, 1985) o en plantaciones de renovación (Caliman et al., 1987). Dufour y Olivin (1985) destacan que los horizontes compactados son bastante evidentes en las interlíneas de siembra, es decir, en las zonas afectadas por el paso continuo de maquinarias, y son tenues o inexistentes en las líneas de siembra o en las paleras (cuando se utiliza el sistema de amontonar las hojas podadas en un sitio específico).

 

El ajuste de los semivariogramas teóricos a los semivariogramas experimentales se realizó visualmente, y se trató de modelar la variabilidad intrínseca del suelo, obviando las irregularidades en el comportamiento de la semivarianza introducidas por la acción antrópica. Los Cuadros 3 y 4 muestran los parámetros de los semivariogramas teóricos ajustados a las variables analizadas en el Ultisol y en el Vertisol, respectivamente. Los modelos utilizados para el ajuste fueron, básicamente, el esférico y el exponencial, y en general se obtuvo un buen ajuste, con rangos de dependencia espacial que van desde 7,80 hasta 39,65 m en el Ultisol, y de 12,28 a 24,32 m en el Vertisol.

 

 

 

Cuadro 3.  Parámetros  de  los  semivariogramas  de  las  propiedades  evaluadas en un Ultisol irrigado cultivado con palma aceitera.
Variable	Modelo	Alcance	Varianza aleatoria	Varianza Total	GDE	R2	Dependencia Espacial
Ks 0-25 cm	Esférico	7,8	0	33,20	0	0,94	Fuerte
Ks 0-50 cm	Exponencial	13,2	15,66	24,07	65,5	0,91	Moderada
Ks 0-Plintita	Esférico	39,6	14,62	40,80	35,8	0,93	Moderada
Ks 0-100  cm	Exponencial	26,4	14,80	53,28	27,8	0,89	Moderada
Da 0-25 cm	Esférico	30,0	0,00189	0,00665	29,1	0,94	Moderada
Da 25-50 cm	Exponencial	23,2	0,00130	0,00545	23,9	0,97	Fuerte
Da 50-75 cm	Esférico	36,0	0,00216	0,00324	66,7	0,95	Moderada
Da 75-100 cm	Exponencial	14,4	0	0,00582	0	0,98	Fuerte
PT 0-25 cm	Esférico	34,1	4,65	8,13	57,1	0,96	Moderada
PT 25-50 cm	Exponencial	22,7	4,27	9,70	44,0	0,92	Moderada
PT 50-75 cm	Exponencial	19,7	1,82	10,78	16,9	0,93	Fuerte
PT 75-100 cm	Exponencial	15,8	6,80	17,60	38,6	0,97	Moderada
Mp  0-25 cm	Esférico	17,6	5,03	6,11	82,3	0,88	Débil
Mp  25-50 cm	Esférico	24,0	3,99	7,77	51,4	0,93	Moderada
Mp 50-75 cm	Exponencial	39,4	1,10	7,67	14,3	0,94	Fuerte
Mp 75-100 cm	Esférico	26,8	3,36	6,55	51,3	0,93	Moderada
GDE = Grado de dependencia espacial; Ks = Conductividad hidráulica saturada; Da = Densidad aparente; PT = Porosidad Total; Mp = Macroporosidad

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cuadro 4. Parámetros  de  los  semivariogramas  de las  propiedades  evaluadas en un Vertisol irrigado cultivado con palma aceitera
Variable	Modelo	Alcance	Varianza aleatoria	Varianza Total	GDE	R2	Dependencia Espacial
Ks 0-25 cm	Esférico	24,32	166,4	650,0	25,6	0,93	Moderada
Ks 0-50 cm	Esférico	20,16	0	291,0	0	0,91	Fuerte
Ks 0-Plintita	Exponencial	17,92	0	235,0	0	0,97	Fuerte
Ks 0-100  cm	Esférico	20,16	0	302,0	0	0,94	Fuerte
Da 0-25 cm	Esférico	21,28	0	254,0	0	0,95	Fuerte
Da 25-50 cm	Esférico	21,28	0	254,0	0	0,96	Fuerte
Da 50-75 cm	Esférico	21,28	0	254,0	0	0,95	Fuerte
Da 75-100 cm	Esférico	21,28	0	254,0	0	0,95	Fuerte
PT 0-25 cm	Esférico	13,28	0	275,0	0	0,96	Fuerte
PT 25-50 cm	Esférico	12,28	0	276,0	0	0,94	Fuerte
PT 50-75 cm	Esférico	14,28	0	289,0	0	0,94	Fuerte
PT 75-100 cm	Esférico	14,28	0	280,0	0	0,93	Fuerte
Mp  0-25 cm	Esférico	20,72	0	236,0	0	0,92	Fuerte
Mp  25-50 cm	Esférico	20,72	0	236,0	0	0,91	Fuerte
Mp 50-75 cm	Esférico	20,72	0	244,4	0	0,93	Fuerte
Mp 75-100 cm	Esférico	20,72	5,1	239,1	2,1	0,93	Fuerte
GDE = Grado de dependencia espacial; Ks = Conductividad hidráulica saturada; Da = Densidad aparente; PT = Porosidad Total; Mp = Macroporosidad

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Un aspecto importante de destacar es que los valores de varianza total para todas las variables del Vertisol fueron notablemente superiores a los de varianza total para el Ultisol. Esta situación demuestra una mayor variabilidad en el Vertisol, lo cual puede estar asociado a cambios en las propiedades del suelo como consecuencia de la expansión y contracción, con los continuos secamientos y humedecimientos del suelo, que dan origen a la formación de grietas.

 

Según los criterios desarrollados por Cambardella et al. (1994), en el Ultisol la dependencia espacial es fuerte para las variables: Ks de 0 a 25 cm, densidad aparente de 25 a 50 cm y desde la plintita hasta los 100 cm, porosidad total de 50 cm hasta la plintita, macroporosidad de 25 a 50 cm y profundidad del estrato de plintita (Cuadro 3). El resto de las variables presentaron una dependencia espacial moderada, a excepción de la variable macroporosidad de 0 a 25 cm, la cual presentó una dependencia espacial débil. En el Vertisol todas las variables presentaron una fuerte dependencia espacial (Cuadro 4), a excepción de la variable Ks de 0 a 25 cm que presentó una dependencia espacial moderada.

 

Cuando se examina el comportamiento de las variables a diferentes profundidades, se encuentra que en el Ultisol (Cuadro 3) los parámetros de los semivariogramas presentan grandes diferencias, lo cual es indicativo de un comportamiento anisotrópico de las propiedades del suelo en los diferentes estratos, que puede ser consecuencia de la distribución de arcilla a través del perfil y/o de las fuerzas mecánicas externas mencionadas con anterioridad.

 

En el Vertisol (Cuadro 4) los parámetros de los semivariogramas, para una misma variable, son similares a las diferentes profundidades, lo cual implica un comportamiento isotrópico de la variabilidad del suelo a través del perfil, aún cuando los valores promedio de la variable sean diferentes.

 

El objetivo final del análisis geoestadístico es la estimación de las propiedades del suelo en los sitios donde no se efectuó la evaluación, lo cual se realiza a través del proceso de interpolación. El método de interpolación más usado en ciencia del suelo es el ‘kriging’ puntual (Trangmar et al., 1985), el cual requiere de un modelo de variación de la variable para realizar las estimaciones.

 

Los parámetros determinados por medio del ajuste de modelos teóricos a los semivariogramas experimentales constituyen el modelo de variación para cada una de las variables evaluadas a las diferentes profundidades de los dos suelos estudiados.

 

A partir de estos parámetros, y asumiendo que la variabilidad del suelo tiene un comportamiento isotrópico en el sentido horizontal, se realizó la interpolación por medio de ‘kriging’ puntual para la variable Ks de 0 a 100 cm, debido a que ésta es considerada una variables integradora y a la vez críticas en el manejo agronómico del cultivo.

 

La Figura 2 muestra el mapa de isolíneas obtenido de la interpolación para la variable Ks de 0 a 100, tanto para el Ultisol (Figura 2A) como para el Vertisol (Figura 2B). Puede observarse que, en ambos casos, las áreas con mayores valores de Ks se ubican hacia las cercanías de los canales de riego o hacia las hileras de siembra (sitios marcados con una cruz en la figura), mientras que las áreas con menores valores de Ks tienden a ubicarse a los largo de la interlínea de siembra (sitios marcados con flechas en la figura), por donde circulan los vehículos y animales de tiro utilizados en las labores de cosecha.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

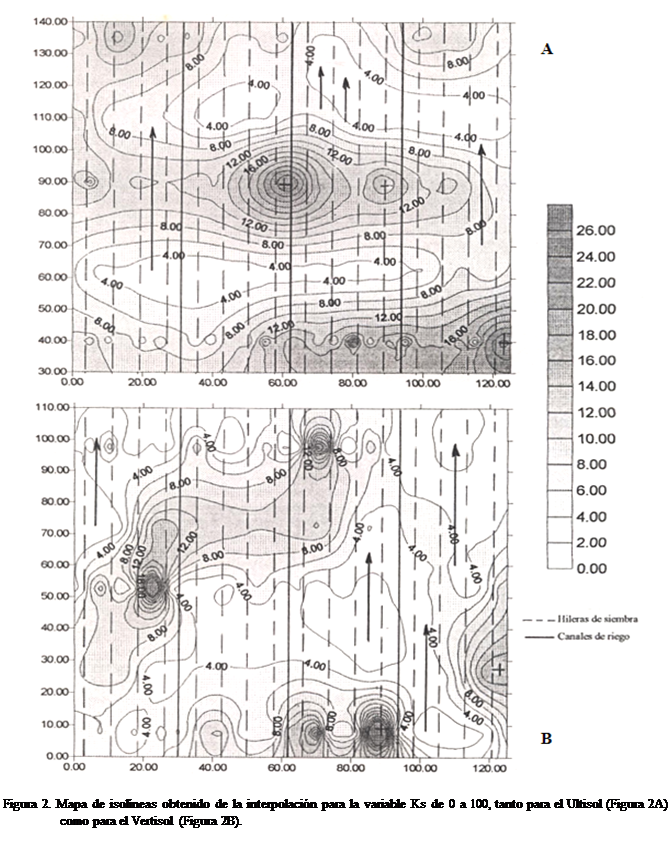
Este comportamiento viene a corroborar la distribución espacial del problema de compactación a lo largo de las interlíneas, derivado del proceso de recolección de frutas a través de carretas movidas por tracción animal tal como los señalan Barrios y Florentino (2008), lo cual representa una clara evidencia de la importancia de la actividad antrópica sobre la variabilidad espacial intrínseca del suelo, llegando a convertirse en la fuente de variación más importante en suelos cultivados.

 

Lo anterior sugiere la implementación del concepto de manejo por sitio específico, apoyado en el uso de mapas que permitan identificar zonas dentro de cada lote con limitaciones importantes que afecten el rendimiento (Bertsch et al. 2002). En tal sentido, una de las estrategias de manejo para optimizar el uso de los recursos productivos, podría orientarse hacia la limitación de los caminos de circulación de vehículos de cosecha, donde se concentrarían las áreas compactadas y se aplicarían correctivos para recuperar aquellas áreas que ya no estarían sometidas a las presiones externas (con el uso de subsolado profundo, por ejemplo).

 

CONCLUSIONES

 

1.    La estructura de los semivariogramas experimentales reveló el impacto de la actividad antrópica sobre las propiedades físicas del suelo, a través de la acumulación de materia orgánica en sitios específicos que incorporan gran variabilidad al horizonte superficial y la formación de capas compactadas en forma localizada que tienden a homogeneizar los horizontes subsuperficiales.

 

2.    Para ambos suelos y para todas las propiedades evaluadas, la estructura de dependencia espacial reveló que la varianza estructurada fue dominante sobre el componente aleatorio del semivariograma, demostrando la utilidad del análisis geoestadístico. Los modelos teóricos ajustados a las propiedades físicas de los suelos fueron del tipo esférico y exponencial.

 

3.    Los mapas de contorno obtenidos por la interpolación por ‘Kriging’ tienen gran importancia en las estrategias de manejo por sitio específico, debido a que indican los lugares donde están concentrados los problemas para la aplicación más eficiente de estrategias preventivas y correctivas.

 

LITERATURA CITADA

 

Ahuja L.; J. Naney and R. Willians. 1985. Estimating soil water characteristics from simpler properties or limited data. Soil Sci. Soc. Am. J. 49: 1100-1105.

 

Bailey T. and A. Gatrell. 1995. Interactive spatial data analysis. Addison Wesley Longman, U. K. 432 p.

 

Barrios R. y A. Florentino. 2008. Propiedades hidráulicas de dos suelos subirrigados cultivados con palma aceitera en el estado Monagas, Venezuela.  Agronomía Tropical 58 (2): 155-162.

 

Blake G. R and K. H. Hartge. 1965. Bulk density. In Methods of soil analysis, Part 1 (A. Klute, ed.), Agronomy Nº 9. Madison, WI. Am. Soc. Agron. p.  371-373. 

 

Bertsch F.; C. Henríquez, F. Ramirez and F. Sancho. 2002. Site-specific nutrient management in the highlands of Cartago province. Better Crops International 16 (1): 16-19.

 

Bregt A.; A. Mcbratney and M Wopereis. 1991. Construction of isolinear maps of soil atributes with empirical confidence limits. Soil Sci. Soc. Am. J. 55: 14-19.

 

Burrough P. 1993. Soil variabilty: a late 20^th century view. Soil and Fertilizers 56 (5): 529-562.

 

Caliman J.; J. Concaret, J. Olivin and F. Dufour. 1990. Maintance of physical soil fertility under oil palm in humid tropical regions. Oleagineux 45 (3): 103-110.

 

Caliman J.; J. Olivin and F. Dufour. 1987. Degradation of sandy ferralitics soil in oil palm  cultivation through compaction. Correction methods. Oleagineux 42 (11): 393-401.

 

Cambardella C.; T. Moorman, J. Novak, T. Parkin, D. Karlen, R. Turko and E. Konopka. 1994. Field-scaled variability of soil properties in Central Iowa Soils. Soil Sci. Soc. Am. J. 58: 1501-1511.

 

Day P. R. 1965. Particle size fractionation and particle size analysis. In Methods of soil analysis, Part 1 (A. Klute, ed.), Agronomy Nº 9.  Madison, WI. Am. Soc. Agron. p. 545-566. 

 

Dufour O. and J. Olivin. 1985. Evolution of soils in oil palm plantation on savannah. Oleagineux 40 (3): 113-123.

 

Englund E. and A. Sparks. 1988. Geo-EAS (Geostatistical Enviromental Assessment Software) User’s guide. EPA. Las Vegas, Nevada. 182 p.

 

Florentino A. 1996. Guía sobre índices físicos de suelo. Valores críticos. Curso de Física de Suelos. Postgrado en Tecnología de Suelo. E.T.S. de Ingenieros Agrónomos. Universidad Politécnica de Madrid. España. Mimeografiado. 20 p.

 

Goovaerts, P. 1997. Geostatistics for natural resources evaluation. Oxford Univ. Press, New York. USA. 487 p.

 

Hamlett J.; R. Horton and A. Cressie. 1986. Resistant and exploratory techniques for use in semivariograms analysis. Soil Sci. Soc. Am. J.  50: 868-875.

 

Henríquez C.; R. Killorn, F. Bertsch y F. Sancho. 2005. La geostadística en el estudio de la variación espacial de la fertilidad del suelo mediante el uso del interpolador kriging. Agronomía Costarricense. Vol. 29 (2): 73-81.

 

Horn R.; H. Domzal; A. Slowinska Jurkiewicz and C. Van Ouwerkerk. 1995. Soil compaction processes and their effects on the structure of arable soils and the enviroment. Soil Tillage Research 35: 23-36.

 

Iqbal J.; J. Thomasson, J. Jenkins, P. Owens and F. Whisler. 2005 Spatial variability analysis of soil physical properties of alluvial soils. Soil Sci. Soc. Am. J. 69: 1338-1350.

 

Jaramillo D. 2006. Efecto de la variabilidad sistemática de la producción de fríjol en experimentos de fertilización. Segunda siembra. Rev. Fac. Nal. Agr. (Medellín) 59 (1): 3147-3165.

 

Jenkins J. R.; D. A. Crouse, R. L. Mikkelsen and R.W. Heiniger 2000. Spatial variability of phosphorus retention capacities for various fields. In: Proceedings of the fifth international conference on precision agriculture. P. C. Robert, R. H. Rust and W. E. Larson (eds). ASA-CSSA-SSSA, Madison, Wisconsin, USA.

 

Journel G. and C. Huibregts. 1978. Mining geostatistics. Academic Press. London, U. K. 600 p.

 

Mallants D.; B. P. Mohanty, D. Jaques and J. Feyen. 1996. Spatial variability of hydraulic properties in a multi-layered soil profile. Soil Science 161 (3): 167-181.

 

Matheron G. 1970. The theory of regionalized variables and its aplications. Cah. 5. Cent. de Morphol. Math., Ecole des Mines de Paris.

 

Mzuku M.; R. Khosla, R. Reich, D. Inman, F. Smith and L. MacDonald. 2005. Spatial variability of measured soil properties across site-specific management zones. Soil Sci. Soc. Am. J. 69: 1572-1579.

 

Obando F.; A. Villegas, J. Betancur y L. Echeverri. 2006. Variabilidad espacial de propiedades químicas y físicas en un Typic Udivitrands, arenoso de la región andina central colombiana.  Rev. Fac. Nal. Agr. (Medellín) 59 (1): 3217-3235.

 

Pannatier Y. 1994. Variowin 2.1: Programs for  spatial data analysis and variogram modeling in 2D. Institute of Mineralogy and Petrography. Univerisity of Lausanne. Switzerland.

 

Peralta F.; O. Vasquez, D. Richardson, A. Alvarado and E. Bornesmiza. 1985. Effect of some soil physical characteristics on yield, growth and nutrition of the oil palm in Costa Rica. Oleagineux 40 (8-9): 423-430.

 

Pérez R. 1987. Estudio agrológico semidetallado del Asentamiento Campesino “El Zamuro”. Palmonagas, C. A. Mimeografiado. 459 p.

 

Pla I. 1983. Metodología para la caracterización física con fines de diagnóstico de problemas de manejo y conservación de suelos en condiciones tropicales. Alcance N^o 32. UCV-Maracay, Venezuela. 93 p.

 

Ramírez López L.; A. Reina Sánchez y J. Camacho Tamayo. 2008. Variabilidad espacial de atributos físicos de un Typic Haplustox de los llanos orientales de Colombia. Eng. Agríc. (Jaboticaba) 28 (1): 55-63.

 

Razuri L. 1978. Reconocimiento del problema de drenaje. CIDIAT. Mérida, Venezuela. Mimeografiado. 112 p.

 

Silva Acuña R.; C. D. Cruz, F. X. R. Vale e L. Zambolim. 1995. PROGRESSA: um programa para estudo das epidemias de doenças de plantas. Fitopatologia Brasileira 20: 368.

 

Trangmar B.; R. Yost and G. Uehara. 1985. Application of geostatistics to spatial studies of soil properties. Advances in Agronomy 38: 45-94.

 

Tukey J. W. 1977. Exploratory data analysis. Addison-Wesley. Reading, MASS. 688 p.

 

Vauclin M.; S. R. Vieira, G. Vachaud and D. R. Nielsen. 1983. The use of co’kriging’ with limited field soil observations. Soil Sci. Soc. Am. J. 47: 175-184.

 

Webster R. and M. A. Oliver. 1990. Statistical methods in soil and land resource survey. Oxford University Press. New York. USA. 307 p.

 

Webster R. and T. M. Burgess. 1980. Optimal interpolation and isarrithmic mapping of soil properties. III. Changing drift and universal ‘kriging’. J. Soil Sci. 31: 505-524.

 

 

 

Página diseñada por Prof. Jesús Rafael Méndez Natera

 

 

 

 

TABLA DE CONTENIDO DE LA REVISTA CIENTÍFICA UDO AGRÍCOLA

 

		Descargar este artículo  en Formato PDF:
			Obtenga el Lector de Archivos PDF