Donwload this paper in PDF format:

 

 

 

 

 

 

 

 

Revista Científica UDO Agrícola Volumen 7. Número 1. Año 2007. Páginas: 15-21

 

Stability analysis of safflower (Carthamus tinctorius L.) lines adaptability in dryland conditions in Iran

 

Análisis de estabilidad de la adaptabilidad de líneas de cártamo (Carthamus tinctorius L.) a condiciones de secano en Irán

 

Khoshnood ALIZADEH DIZAJ

 

Oilseed, Food and Feed Legumes Department. Dryland Agricultural Research Institute, PO Box 119, Maragheh, Iran. Telephone: +98 (421) 2228078. Fax: +98 (421) 2222069. E Mail: khoshnod2000@yahoo.com

 

 

ABSTRACT

 

Spatial variability is inherent in all field trials. The selection efficiency of the most desirable safflower genotypes can be improved by identifying the underlying spatial patterns in field trials and by incorporating these into the statistical analysis. The main objective of this study was to evaluate the grain yield stability of 25 safflower lines after adjustment for spatial variability across a series of simple lattice designed trials at five research stations over a three years period. There was spatial variability in 50% of the trials. For most of the environments tested in this study, the use of complete blocks to account for variability was more efficient than incomplete blocks. Three types of spatial analysis were effective in accounting for variability: 1) randomized complete block design with first order auto-correlated errors along rows, 2) lattice design with correlated errors along rows as well as columns and 3) randomized complete block design with first order auto-correlated errors in plots along rows and along columns. Two genotypes (287 and 79-299) had the best stability, using the environmental coefficient of variation. However, these were also amongst those with the lowest yields. Yet, when the regression coefficient (b) on the basis of best linear unbiased estimates of grain yield was used, genotypes 367 and PI250596 were the most stable. It is recommended that first a best model be identified to describe the spatial variation in data, followed by evaluation of the genotypes based on that model.

 

Key words: Carthamus tinctorius, genotype x environment interaction, spatial analysis.

 

RESUMEN

 

La variabilidad espacial es inherente en todos los ensayos de campo. La eficiencia de la selección de los genotipos más deseables del cártamo puede mejorarse identificando los patrones espaciales subyacentes en los ensayos de campo e incorporando éstos en el análisis estadístico. El objetivo principal de este estudio fue evaluar la estabilidad del rendimiento de semillas de 25 líneas de cártamo después del ajuste de la variabilidad espacial a través de una serie de ensayos diseñados en un láttice simple en cinco estaciones de investigación en un período de tres años. Hubo una variabilidad espacial en el 50% de los ensayos. Para la mayoría de los ambientes evaluados en este estudio, el uso de bloques completos para explicar la variabilidad fue más eficiente que los bloques incompletos. Tres tipos de análisis espacial fueron efectivos para explicar la variabilidad: 1) diseño de bloques completos al azar con errores de primer orden autocorrelacionados a lo largo de las hileras, 2) diseño de láttice con errores correlacionados a lo largo de las hileras así como de las columnas y 3) diseños de bloques completos al azar con errores de primer orden autocorrelacionados a lo largo de las hileras y de las columnas. Dos genotipos (287 y 79-299) tuvieron la mejor estabilidad, usando el coeficiente de variación ambiental. Sin embargo, éstos estuvieron también entre aquellos con los rendimientos más bajos. Aún, cuando se usó el coeficiente de regresión (b) basado en las mejores estimaciones lineales no sesgadas del rendimiento de semillas, los genotipos 367 y PI250596 fueron los más estables. Se recomienda que primero se identifique el mejor modelo para describir la variación espacial en los datos, seguido por la evaluación de los genotipos basada en ese modelo.

 

Palabras clave: Carthamus tinctorius, interacción genotipo x ambiente, análisis espacial.

 

 

INTRODUCTION

 

Development of oilseed crops has gained a high priority in Iranian agriculture in recent years. Drylands occupy over 6.2 million hectares of arable lands across the country. Preliminary trials have indicated that safflower (Carthamus tinctorius) is the oilseed crop best adapted to the low rainfall and stress conditions of Iranian dryland (Rashid et al., 2002). In the regional crop variety testing trials, more than 150 domestic and exotic lines of safflower have been evaluated over eight years for grain yield in the Dryland Agricultural Research Institute (DARI), Maragheh, Northwest Iran (Alizadeh, 2003). The relative performance of lines varies with environment, and this genotype´environment (GxE) interaction hampers selection of lines for cultivation over a wide region. In addition, field trials are often conducted in fields that are quite heterogeneous due to biotic and abiotic factors, including topography and soil fertility. The fact that crop response varies within a field, due to underlying crop growth processes and their responses to concomitant soil process variables in space (Nielsen et al., 1994) and time (Stafford, 1999), is a dilemma to soil and crop scientists (Cassel et al., 2000). Although experimental designs usually account for a large section of heterogeneity in the field, a considerable amount of variation within the blocks may remain unaccounted for by traditional methods of analysis, especially as trial size increases as more genotypes are tested.

 

Modern methods of analysis can further help to reduce this unaccounted component of variability (Singh, 2002). The best method should have the ability to explain data according to a standard statistical criterion. Spatial variability arises from both variation in soil properties and distribution (i.e. natural variation) and experimental procedure (i.e. extraneous variation) such as effects of serpentine harvesting of plots and variation due to unequal plot lengths arising from inaccurate trimming (Gilmour et al., 1997). An effective evaluation of cultivars can be made by identifying and understanding both the underlying spatial pattern of experimental material and incorporating these patterns into the statistical analysis. Spatial analyses have been reported for cereals (Cullis and Gleeson, 1991; Grondona et al., 1996; Gilmour et al., 1997; Wilkinson et al., 1983) and pasture (Sarker et al., 2001).

 

Various statistical models have been presented in the literature to study GxE interactions (Becker, 1981; Eberhart and Russell, 1966; Finlay and Wilkinson, 1963; Kempton, 1984; Lin et al., 1986; Plaisted and Peterson, 1959; Perkins and Jinks, 1968). The multitude of concepts and measures of stability has been developed based on the variety of different outlooks of experimenters and the uniqueness of their specific problems. For example, Smith et al. (2001) used multiplicative mixed models and adjustments for spatial field trends, while Feyerherm et al., (2004) constructed statistical method for producing probabilistic inferences of future yielding ability from a sample of cultivar performance trials. However, the author is unaware of any reports on the use of spatially-adjusted means for stability analysis in any crop system.

 

The analyses detailed in this study were designed to (i) evaluate the spatial variability in safflower field trials, (ii) study the adaptation of these lines using some stability parameters on mean grain yields of safflower after adjusting for spatial variability and (iii) suggest selections made using this approach amongst 25 varieties from 13 field test environments.

 

MATERIALS AND METHODS

 

Twenty-five safflower pure lines (Table 1), developed at the Dryland Agricultural Research Institute, were evaluated over a three year period (2000 to 2003) across five Research Stations in Iran and there were 13 growing environments in total, because on two sites (Kurdistan and Maragheh) investigations were performed for two years (Table 2). The individual trials were conducted using a square lattice design with 2 replications. The experiments were planted in the late autumn of each year just before the first frost in each region. Each genotype was sown in plots (9 m²) of 6 rows, 5-m long, with spacing of 30-cm between rows. Each plot was harvested leaving 30 cm on both ends of the rows in order to exclude border effects.

 

Table 1. Origin of the 25 genotypes of safflower (Carthamus tinctorius L.).
No.	Genotype	Origin
1	287	Iran
2	79-299	Iran
3	301	Iran
4	336	USA
5	338	Syria
6	342	USA
7	348	USA
8	350	Canada
9	356	Cyprus
10	361	Pakistan
11	367	Kenya
12	368	Spain
13	372	Pakistan
14	375	Pakistan
15	376	Pakistan
16	405	Syria
17	406	Turkey
18	411	Iran
19	412	Iran
20	415	Iran
21	Cyprus	Cyprus
22	Zarghan	Iran
23	PI250596	USA
24	PI250537	Canada
25	PI258417	Iran

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Table 2. Location, elevation and meteorological data for the five research sites in Iran.
Site	Env.	Location	Elevation (m)	Year	Prec. (mm)	Mean Abs. Max. T (°C)	Mean Abs. Min. T (°C)	No. of days below 0°C
Shirvan	1	57° 55¢ N, 37° 23¢ E	1086	2000-2001	186	17	3.2	89
	2			2001-2002	329	20	1.2	65
	3			2002-2003	302	10.5	1.5	98
Kurdistan	4	47° 0¢ N, 35° 20¢ E	1500	2001-2002	350	17	0.8	104
	5			2002-2003	382	8	0	119
Kermanshah	6	34° 20¢ N, 47° 20¢ E	1351	2000-2001	432	18	3.55	79
	7			2001-2002	413	21	2	76
	8			2002-2003	424	14	1.5	76
Ilam	9	46° 25¢ N, 33° 38¢ E	1363	2000-2001	413	22	4	11
	10			2001-2002	627	23	5	13
	11			2002-2003	474	24	5.3	15
Maragheh	12	37° 15¢ N, 46° 20¢ E	1720	2001-2002	381	18	1	114
	13			2002-2003	367	8.5	0	134
Env.: Growing environment; Prec.: Precipitation; Mean Abs. Max. T: Mean absolute maximum temperature; Mean Abs. Min. T: Mean absolute minimum temperature

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Eighteen models covering a range of spatial patterns were generated for analyzing the grain yield from each trial (Singh, 2002). The components of spatial patterns comprised factorial combinations of block structures, trends and structures for plot errors (Table 3).

 

 

Table 3. List and abbreviations of models used to describe spatial variability in randomized complete block design (Rc) or lattice design (Lt).
Error/ Trends	Abbreviation
Independent plot errors	Rc (or Lt)
First order auto-regressive errors along rows	Rc (or Lt)Ar
First order auto-regressive error along rows and along columns	Rc (or Lt)ArAr
Fixed linear trend along rows	Rc (or Lt)L
Fixed linear trend along rows and first order auto-regressive errors along rows	Rc (or Lt)LAr
Fixed linear trend along rows and first order auto-regressive error along rows and along columns	Rc (or Lt)LArAr
Random cubic spline in column number (including linear trend)	Rc (or Lt)Cs
Random cubic spline in column number and first order auto-regressive errors along rows	Rc (or Lt)CsAr
Random cubic spline in column number and first order auto-regressive error along rows and along columns	Rc (or Lt)CsArAr

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Genotype effects were assumed to be fixed parameters, while replication effects and block effects within  replications   were   assumed   to   be   random variables. Parameters were estimated using the residual maximum likelihood (REML) method in Genstat 5 Release 4.1 (1997). The REML directive produced a statistic, called the deviance (Dev), which facilitated the computation of the Akaike (1974) criterion (AIC). The deviance is minus twice the REML log-likelihood ignoring a constant depending on the fixed terms. Since the maximum log-likelihood value is expected to increase with the number of parameters, this criterion decreases this value by introducing a penalty in terms of the number of unknown parameters of the variance-covariance of the error components. Thus the AIC is based on a penalized log-likelihood, where the penalty increases with the number of variance-covariance parameters in the fitted spatial structure. A comparison of models with the same set of fixed effects was carried out using the AIC. When expressed in terms of the deviance values, this can be defined as: AICD= Dev + 2N, where N is the number of linear and non-linear variance components of the models.

 

The model with the lowest AICD value was deemed to be the best, due to goodness of fit of that model over others (Singh, 2002). The significance of the fixed linear trend was tested using the Wald statistic (Genstat 5 committee, 1997). This is computed as the ratio of the squared estimate of the linear trend to its estimated variance and follows a chi-square distribution in the absence of a trend. If the trend is statistically significant at P ≤ 0.05, then the best  model  is  chosen from models including a linear trend factor. For each trial, the best model was used to compute the efficiency of the method of analysis This was assessed by comparing the average variance of pair-wise genotype comparisons with that of a randomized complete block design with independent errors (i.e. no spatial errors) as following:

 

 

 

 

 

 

 

The best model was identified as describing the spatial variation in the data. Finally, evaluations of the genotypes were made using a combination of the spatially adjusted best model and the stability analysis from the best linear unbiased estimates (BLUEs). The stability indices suggested by Francis and Kannenberg (1978) (CV) and Finlay and Wilkinson (1963) (b) were calculated as following using MS Excel.

 

 

 

 

 

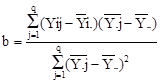
Where, Y_ij denotes the mean value of i-th genotype in the j-th environment.

 

RESULTS

 

Spatial analysis of the data revealed no evidence for the existence of fixed errors in these trials since the Wald statistics were not significant across all environments (environment 1 in Table 4). Hence, the best models were selected amongst the first 6 out of 18 models, which did not contain the fixed errors with regard to the AICD statistic. Various statistics for environment 1 are shown in Table 4 in order to illustrate the process by which the best model was selected. Among the six selected models, the best model for environment 1 was RcArAr which has the lowest AICD (Table 4). A summary of the best models along with their efficiency over the randomized complete block design for all environments are listed in Table 5. In the environments numbered 1, 2, 5, 6, 9 and 11, plot errors were found to be correlated either along rows or along both rows and columns. Incomplete blocks (lattice design) were less effective than complete blocks in all trials, except for environment 6 (Table 5). In most trials, the randomized complete block design was identified as optimal (Table 5).

 

 

Table 4. Information based on the Akaike criterion expressed in terms of deviance values (AICD) to select the best model for safflower trial in environment 1.
Model	q	Df	AICD	Walda
Rc	2	23	270.06	-
RcAr	3	22	268.38	-
RcArAr	4	21	264.71	-
Lt	3	22	268.30	-
LtAr	4	21	268.20	-
LtArAr	5	20	267.54	-
RcL	2	22	265.21	0.01
RcLAr	3	21	263.26	0.14
RcLArAr	4	20	259.48	0.01
LtL	3	21	263.37	0.08
LtLAr	4	20	262.97	0.31
LtLArAr	5	19	262.05	0.90
RcCs	3	21	265.21	0.00
RcCsAr	4	20	263.26	0.14
RcCsArAr	5	19	259.48	0.01
LtCs	4	20	263.37	0.08
LtCsAr	5	19	262.94	0.31
LtCsArAr	6	18	262.46	0.92
Abbreviations used for spatial models are defined in Table 3. q: number of variance components in the model.   Df: residual degrees of freedom. aWald statistics for testing for a linear trend along rows.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Table 5. Best models, efficiency over randomized complete block design in thirteen safflower trials in dryland condition.
Environment No.	Best model	Efficiency (%)
1	RcArAr	177
2	RcAr	127
3	Rc	100
4	Rc	100
5	RcArAr	148
6	LtArAr	451
7	Rc	100
8	Rc	100
9	RcArAr	82
10	Rc	100
11	RcAr	98
12	Rc	100
13	Rc	100
Environments are defined in Table 2. Abbreviations used for spatial models are defined in Table 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Unadjusted means along with average best linear unbiased estimates of grain yield over the environments and some stability parameters including coefficient of variation (CV), regression coefficient (b) and coefficients of determination (r²) are presented in Table 6. The unadjusted mean genotype grain yield over all environments ranged from 851 kg/ha to 1271 kg/ha, whereas the observed range for adjusted means was 920-1411 kg/ha and 12 lines had mean grain yield above the grand mean (1137 kg/ha). To demonstrate interrelationship of the stability statistics estimated, correlation coefficient between genotype ranks obtained from used stability indices and mean grain yield were calculated (Table 7). A significant positive rank correlation was obtained between genotype means, b and r².

 

 

Table 6. Average safflower grain yield (kg/ha) in all environments (Mean) along with mean best linear unbiased estimates (BLUE) and estimates of common stability indices.
Genotypes No.	Unadjusted Mean	BLUE	CV	b	r2
1	907	923	0.77	0.60**	0.90
2	958	1028	0.88	0.80**	0.99
3	1120	1204	1.13	1.19*	0.95
4	1114	1217	1.17	1.21	0.91
5	1116	1191	1.03	1.04	0.90
6	1271	1411	1.16	1.42**	0.94
7	939	1013	0.95	0.78	0.81
8	957	1043	0.88	0.78*	0.90
9	912	1015	0.99	0.85	0.89
10	936	1037	0.88	0.79**	0.94
11	1141	1219	0.94	1.01	0.96
12	1116	1213	1.14	1.22**	0.98
13	1073	1211	1.26	1.26	0.86
14	905	977	0.92	0.75*	0.87
15	1028	1107	0.96	0.93	0.97
16	1163	1245	1.09	1.21**	0.98
17	1025	1114	1.17	1.15*	0.98
18	945	1040	1.00	0.90	0.95
19	851	920	0.93	0.74**	0.93
20	1002	1109	1.07	0.97	0.84
21	1212	1326	0.95	1.10	0.95
22	1197	1311	1.09	1.27**	0.99
23	1097	1218	0.99	1.07	0.98
24	982	1053	0.98	0.86	0.88
25	1190	1288	1.01	1.13	0.94
LSD 5%	112	123
Genotypes are defined in Table 1. CV: Coefficient of variation b:   linear response to changes in environments r2: Coefficient of determination. * Significantly different from 1.0 at the P ≤ 0.05.  ** Significantly different from 1.0 at the P ≤ 0.01. LSD: Least Significant Difference

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Table 7. Correlation between genotype ranks on the basis of mean grain yield (Mean) and stability indices.
	Mean	CV	b
CV	0.60 **
b	0.88 **	0.88 **
r2	0.44 *	0.13	0.41 *
CV: Coefficient of variation.    b: linear response to changes in environments. r2: Coefficient of determination.  * and ** Significant at P ≤ 0.05 and P ≤ 0.01, respectively.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

DISCUSSION

 

In all but one of the trials, the use of complete blocks to account for variability had higher efficiency than incomplete blocks (Table 5). Irrespective of the specific form of the model, and acknowledging that the spatial variability of each field is unique (Gilmour et al., 1997), because of relatively high numbers of genotypes, lattice design was expected to be more efficient. However, the models based on complete blocks and first order auto-regressive errors were frequently found to give an improvement in our field trials during these years.

 

There was no evidence of fixed linear trend along rows or random cubic splines in columns. It may be concluded that natural variation, which may result in ‘linear trend’ according to Gilmour et al. (1997), could be well described by blocking in our experiments. Meanwhile, if a larger number of trials were examined, the situation may change and other patterns of spatial variability might become evident. Sarker et al. (2001) reported all spatial variability models in 53 lentil trials. Since the selected models accounted most effectively for spatial variability, they would therefore enhance the breeding efficiency in the selection of the desired genotypes.

 

Wide adaptation is important for safflower in dryland conditions, because of the wide range of environments encountered. Environmental coefficient of variation (CV), as Type 1 stability index (Lin et al., 1986), may be considered relevant for this purpose. A highly significant positive rank correlation was obtained between CV and mean grain yield indicating that lower CVs were accompanied by lower grain yields (Table 7). This was expected according to Becker (1981). Although wide adaptation may be desirable, it is difficult to achieve in practice (Becker, 1981). In terms of CV, genotypes 287 and 79-299 were amongst those with the highest stability (lowest CV), but they were amongst those which produced the lowest yields (Table 6). On the other hand, Lin et al. (1986) noted that when variability in response can be satisfactorily expressed by a regression model, the regression coefficient (b) can serve as a stability parameter and could be preferred to other parameters. The values of the coefficients of determination (r²) from individual linear regression analysis ranged from 0.81 to 0.99 (Table 6). Hence the regressions accounted for quite a large amount of the variation across environments. However, it should be denoted that the regression is partly auto correlated and the slope is very much determined by the yield in the high yielding environments.

 

 Furthermore, the regression coefficient provides information on the shape of response along with its variation. Linear responses to changes in environments (b) ranged from 0.6 to 1.42 (Table 6). The large variation in regression coefficients indicates that some of the 25 entries responded differently to varying environmental conditions. Seven genotypes showed average stability (i.e. regression coefficients did not differ significantly from 1.0) with the grain yield above the grand mean, indicating that they have general adaptability (Table 6). Amongst these seven entries, genotypes 367 and PI250596 had some of the lowest CV values (Table 6) which were selected for use in on-farm trials for demonstration.

 

CONCLUSIONS AND RECOMMENDATIONS

 

Two genotypes (287 and 79-299) had the best stability with rather low grain yield which may be suitable for marginal lands. When the regression coefficient (b) on the basis of best linear unbiased estimates of grain yield was used, genotypes 367 and PI250596 were the most stable lines for dryland conditions. Regarding efficiencies of best models over the randomized complete block design and since the criterion used was based on maximum information in the data and a penalty function, the inferences drawn from the best model could give most realistic assessment of the stability of genotypes. Hence, it is recommended that to evaluate safflower genotypes first a best model be identified to describe the spatial variation in the data, and then the evaluation of the genotypes should be made using it.

 

ACKNOWLEDGMENT

 

I would like to thank M. Singh from the International Center for Agricultural Research in the Dry Areas (ICARDA) for his kind advice and help in statistical analysis. The collaborations of M. Eskandari, H. Hatamzadeh, A. Shariati and M. P. Siahbidi at different Research Stations of Iran are greatly acknowledged. 

 

LITERATURE CITED

 

Akaike, H. 1974. A new look at the statistical model identification. Rothamsted Experimental Station, Harpenden, Herts, UK. 233 p.

 

Alizadeh, Kh. 2003. Oilseed crops for cold drylands of Iran. In: Proceeding of 7^th International conference on development of dry lands. Tehran, Iran. p. 33-34.

 

Becker, H. C. 1981. Correlations among some statistical measures of phenotypic stability. Euphytica 30: 835-840.

 

Cassel, D. K., O. Wendroth and D. R. Nielsen. 2000. Assessing spatial variability in an agricultural experiment station field. Agron. J. 92: 706-714.

 

Cullis, B. R. and A. C. Gleeson, 1991. Spatial analysis of field experiments - an extension to two dimensions. Biometrics 47: 1449-1460.

 

Eberhart, S. A. and W. A. Russell. 1966. Stability parameters for comparing varieties. Crop Sci. 6: 36-40.

 

Feyerherm, A.; G. Paulsen and A. Fritz. 2004. A statistical method for summarizing results of cultivar performance trials. Agron. J. 96: 992-996.

 

Finlay, K. W. and G. N. Wilkinson, 1963. The analysis of adaptation in a plant breeding programme. Australian J. of Agric. Res. 14: 742-754.

 

Francis, T. R. and L. W. Kannenberg. 1978. Yield stability studies in short-season maize. 1. A descriptive method for grouping genotypes. Canadian J. of Plant Sci. 58: 1029-1034.

 

Genstat 5 Committee. 1997. Genstat 5 Release 4.1, Reference Manual Supplement, Lawes.

 

Gilmour, A. R.; B. R. Cullis and A. P. Verbyla. 1997. Accounting for natural and extraneous variation in the analysis of field experiments. J. of Agric., Bio. and Env. Stat. 2: 269-293.

 

Grondona, M. O.; J., Crossa; P. N. Fox and W. H. Pfeiffer. 1996. Analysis of variety yield trials using two-dimensional separable ARIMA processes. Biometrics, 52: 763-770.

 

Kempton, R. 1984. The use of biplots in interpreting variety by environment interactions. J. of Agric. Sci. 103: 123-135.

 

Lin, C. S.; M. R. Binns and L. P. Lefkovitch. 1986. Stability Analysis: where do we stand? Crop Sci. 26: 894-900.

 

Nielsen, D. R.; O. Wendroth and M. B. Parlange. 1994. Developing site-specific technologies for sustaining agriculture and our environment. In: Narayanasamy, G. (Ed.).Management of land and water resources for sustaining agriculture and our environment. Indian Society of Soil Science, New Delhi. p. 42-47.

 

Perkins, J. M. and J. L. Jinks. 1968. Environmental and genotype-environment components of variability. Heredity 23: 339-356.

 

Plaisted, R. L. and  L. C. Peterson. 1959. A technique for evaluating the ability of selections to yield consistently in different locations or seasons. Am. Potato J. 36: 381-385.

 

Rashid, A.; A. Beg; A. A. Attary; S. S. Pourdad and Kh. Alizadeh. 2002. Oilseed crops for the highlands of CWANA. ICARDA Caravan 16:27-29.

 

Sarker, A.; M. Singh and W. Erskine. 2001. Efficiency of spatial methods in yield trials in lentil (Lens culinaris ssp. culinaris). J. of Agric. Sci. 25: 312-319.

 

Singh, M. 2002. GENSTAT Programs for Spatial Analysis of Variety Trials. ICARDA Biometric Report No. 2, Aleppo, Syria. 38 p.

 

Smith, A.; B. Cullis and R. Thompson. 2001. Analysing variety by environment data using multiplicative mixed models and adjustments for spatial field trend. Biometrics 57: 1138-1147.

 

Stafford, J. V. 1999. An investigation into the within-field spatial variability of grain quality. In: J.V. Stafford (Ed). Proceeding of 2^nd European Conference on Precision Agriculture. Sheffield Academic Press, UK. p. 353-361.

 

Wilkinson, G. N.; S. R., Eckert; T. W. Hancock and O. Mayo. 1983. Nearest neighbor (NN) analysis of field experiments. J. of Royal Stat. Soc. 45: 152-212.

 

 

 

Página diseñada por Prof. Jesús Rafael Méndez Natera

 

 

 

TABLA DE CONTENIDO DE LA REVISTA CIENTÍFICA UDO AGRÍCOLA

 

 

			Donwload this paper in PDF format:
		Get the PDF file reader