Revista Científica UDO Agrícola Volumen 11. Número 1. Año 2011. Páginas:
109-125
Distribución
espacial en poblaciones de Oebalus insularis Stal (Hemiptera: Pentatomidae) en el cultivo de arroz en Calabozo, estado
Guárico, Venezuela
Spatial distribution in
populations of Oebalus insularis Stal (Hemiptera: Pentatomidae) in rice in Calabozo, Guárico
State, Venezuela
Luis Enrique VIVAS C. 1  y Armando NOTZ 2
y Armando NOTZ 2
1Centro de investigaciones Agrícolas del Guárico (CIAE-Guárico), Instituto Nacional de Investigaciones
Agrícolas (INIA). Carretera Nacional Calabozo-San
Fernando de Apure, Km. 28. Banco de San Pedro, Calabozo, estado Guárico.
Venezuela y 2Universidad Central de Venezuela, Facultad de Agronomía, Maracay, estado Aragua, Venezuela. E-mails: lvivas@inia.gov.ve, lvivas18@yahoo.es y anotz@cantv.net  Autor
para correspondencia
Autor
para correspondencia
|
Recibido: 28/10/2009 |
Fin de primer arbitraje:
08/10/2010 |
Primera revisión recibida: 10/12/2010 |
Aceptado: 05/02/2011 |
RESUMEN
Se realizaron
estudios en campos de arroz con riego ubicados en tres
parcelas del Sistema de Riego Río
Guárico entre los años 2001 a 2004. El objetivo de este trabajo fue determinar
la distribución espacial de la chinche vaneadora del grano de arroz, Oebalus insularis
Stal., en
campos de arroz. Las características poblacionales fueron estimadas mediante la
relación s2/, índice
de Morissita; la
ley de potencia de Taylor, el índice de Iwao y el
modelo matemático de la binomial negativa. La chinche en su estado
adulto presentó una distribución en el campo del tipo agregada o contagiosa, ajustándose al modelo matemático de la binomial negativa.
Palabras clave: Oryza sativa, Oebalus insularis, distribución espacial, modelo.
ABSTRACT
Studies were conducted on irrigated in three rice fields located at the Rio
Guárico Irrigation System in Calabozo, Venezuela,
between 2001 and 2004. The objective was to determine the spatial distribution
of Oebalus insularis Stal in rice fields. The population characteristics
were studied by using to s2/ relations, Morissita index and Taylor´s power
law and Iwao´s index. The insect’s field spatial
distribution was aggregated or contagious. The population distribution adjusted
to the negative binomial mathematical model.
Key words: rice, Oryza sativa, Oebalus insularis, spatial distribution, models.
INTRODUCCIÓN
El arroz (Oryza sativa) es uno de los
cultivos más importante en el mundo, se produce en 113 países; representando el
alimento básico de la dieta alimenticia de más de la mitad de la población
mundial (FAO 2006, Gramene 2006). En Venezuela, el consumo per
cápita de arroz es de 15 kg/año (ACA 2005); La
producción para el año 2005 fue 950.000 toneladas, con un rendimiento promedio
de 5 t/ha, en una superficie de 190.000 ha (FAOSTAT
2006). En el país, el 90% de la producción se concentra en los estados
Portuguesa y Guárico con pequeños aportes de Barinas y Cojedes (Vivas et al. 2002; Vivas 2008; Vivas y Notz
2009).
Las pérdidas causadas por plagas
representan una de las mayores limitantes en el incremento de la productividad
del arroz, causando un aumento significativo de los costos de producción
(Dávalos 1997 citado por Labrín, 2007). En el mundo,
se estima que las plagas destruyen cerca del 35% de la producción de arroz, de
las cuales 12% son causadas por insectos plagas (Pantoja et al 1997; Vivas et al. 2002; Vivas 2008; Vivas y Notz 2009).
Entre las plagas más importantes del
arroz bajo riego en Venezuela se encuentra la chinche vaneadora
del arroz, Oebalus
spp., de la familia Pentatomidae.
(Aponte et al., 1992, 1997; Sánchez,
1995; Vivas, 1997b, 1999, 2002). Tanto los adultos como las ninfas causan daño al
alimentarse de la panícula ya que los granos al ser succionados pueden quedar
total o parcialmente vacíos o quebrarse en el momento de la molienda; lo cual
ocasiona pérdidas en el rendimiento y calidad del grano. (Adams et al.
1990; Andrews y Quezada, 1989; Aponte et al.,
1997; Daza, 1991; Drees, 1996; Gómez y Meneses, 1985; Guharay, 2002; Gutiérrez et al., 1985, 1987, 1991; Meneses et al., 1995, 2001; Narres y Smith, 1984; Portal et al.,1978; Red de mejoramiento de arroz para el Caribe, 1991; Viator et al.,
1983; Vivas, 2002; Weber, G. 1989). Estos
insectos se encuentran generalmente causando daños en la época de lluvia en las
zonas tropicales y durante la fase de maduración del grano en las principales
zonas arroceras de América (Aponte et al. 1997; Daza, 1991; Gómez y
Meneses, 1980, 1985; Pantoja et al.,
1997; Red de mejoramiento de arroz para el Caribe, 1991; Vivas, 2008).
La distribución espacial de las
poblaciones es una de las características ecológicas más importantes e
indispensables para que sea muestreada eficientemente (Ruesink
y Kogan 1982), ya que afecta la estimación de la
media poblacional (Southwood 1978) y determina
parámetros específicos que permiten la separación de
las especies, pues dicha distribución representa las expresiones poblacionales
del comportamiento de los individuos que las conforman (Taylor 1984). A tal
fin, se puede definir que una población se distribuirá al azar, cuando
cualquier lugar del espacio tiene la misma probabilidad de ser ocupado por un
individuo de la población, sin que esta ocupación afecte la ubicación de otros
individuos pertenecientes a la misma población. Este tipo de distribución se
caracteriza porque la media () obtenida a
través de muestreos, es igual a la varianza (S2)
calculada a partir de las diferentes muestras. La distribución espacial será
agregada en aquellos casos en los cuales la presencia de un individuo genera
una mayor probabilidad de encontrar en las cercanías otros de la misma
población, por lo tanto la de las muestras
tiende consistentemente a ser menor que la S2
de las mismas. La distribución es uniforme, cuando los individuos son
encontrados siguiendo un patrón regular, de manera tal que localizar un
ejemplar disminuye la probabilidad de encontrar
otro en las cercanías. En este caso, la de las muestras es
mayor que la S2 (Clavijo, 1993).
Clavijo (1993), plantea dos
tipos de errores que pueden afectar la determinación de la distribución
espacial de las poblaciones de insectos. El primero, debido al rápido
crecimiento de dichas poblaciones, genera cambios en la densidad de las mismas,
que a su vez se traducirán en cambios en los valores de los parámetros
utilizados para la determinación de la distribución espacial, y el segundo,
consecuencia del primero, representado por la extrapolación de información y
conclusiones en relación a la distribución espacial fuera de los límites
establecidos por las condiciones en que se obtuvieron los parámetros usados
para la determinación de la misma.
Fye citado por Clavijo (1993) señala que muchas de las
muestras de insectos presentes en algodón tienen una distribución agregada y
son descritas por la distribución de probabilidad binomial negativa; sin
embargo, algunas otras se ajustan a la distribución de probabilidad Poisson, lo que sugiere una distribución al azar.
Clavijo (1978a)
menciona que al trabajar con larvas del gusano cogollero del maíz, Spodoptera frugiperda
J.E. (Smith), determinó una distribución al azar para
la población de larvas (grandes y medianas) contadas en las plantas, sin
separar ni extraer la parte terminal o cogollo. García (1982) confirma los
resultados para larvas grandes y medianas de S. frugiperda
y estima la distribución para la población de
larvas pequeñas la que resulta agregada y responsable de la distribución de la
población de larvas, cuando ésta se estima descartando el criterio de tamaño. Segnini (1984) encontró que Empoasca
kraemeri Ross y Moore (Homoptera:
Cicadellidae) presentaba variaciones en la
distribución espacial de sus poblaciones tanto en relación a la época de
cultivo como en cuanto a la fase de insecto involucrada en la estimación; En el
caso de los adultos, la distribución espacial resultó al azar cuando sus
densidades fueron muy bajas, situación frecuente al inicio del cultivo
(invasión) y hacia el final del mismo (emigración). El resto del tiempo los
adultos, así como los huevos y las ninfas, presentaron una distribución
agregada.
Vivas (1997a)
determinó que los adultos del insecto sogata, Tagosodes orizicolus
Muir, presentaron una distribución agregada
en la mayoría de las evaluaciones realizadas, mientras que el resto de los
datos que no siguieron la distribución agregada coinciden con los de una
distribución al azar. Por otro lado, las poblaciones de ninfas se aproximaron a
la distribución al azar.
Foster et al., 1989 y Espino et al.,
2008 demostraron que la especie O. pugnax se distribuye en campo de forma agregada en
los estados de Florida y Texas, probando varios índices para tal fin y métodos
de muestreo que incluyen la malla entomológica y métodos visuales.
Daza (1991) en Colombia, menciona para
las especies O. insularis y O. ornatus, que no existen patrones de agregación dentro
del campo y las mayores poblaciones se encuentran durante el período de
maduración del cultivo. Así mismo, los muestreos realizados en tres áreas del
campo (borde, intermedio y centro) indicaron que los chinches se encontraron distribuidos al azar, lo cual sugiere que los
muestreos se pueden realizar en cualquier área del campo (Daza, 1991; Pantoja et al., 1997).
El objetivo del trabajo fue determinar la
distribución espacial del estado adulto de la chinche vaneadora
del grano Oebalus insularis en tres parcelas del sistema de riego río
Guárico (S.R.R.G.) por cuatro años consecutivos.
MATERIALES Y
MÉTODOS
Se empleó la
información proveniente de las parcelas 152, 173 y un lote del INIA Guárico ubicadas en el S.R.R.G
en Calabozo estado Guárico para determinar la distribución espacial del estado
adulto de O. insularis.
Durante las evaluaciones desarrolladas en este trabajo de investigación,
se tomaron tres parcelas por año (4 años), a las cuales se les practicó
muestreos semanales por medio de la malla entomológica (5 pases dobles de malla
por punto) y 10 puntos en cada parcela seleccionada. Las evaluaciones se
realizaron a lo largo de dichas parcelas y a una distancia de 3 a 5 metros de
las lomas de los paños evaluados. Para la revisión y conteo de la población de
insectos en cada parcela, se tomaron lotes de 5 hectáreas, a los cuales se les
realizaron las practicas agronómicas típicas de la zona (control de malezas,
hectáreas, fertilización, riego y en los lotes de las parcelas estudiadas, no
se aplicó control químico de insectos plagas). (Vivas, 1997a;
2008). Para el análisis estadístico, se emplearon los paquetes de computación InfoStat (2004) y Statixtix
(1990) empleando la prueba no parámetrica de Kruskal-Wallis, y
usando como factores o fuentes de variación de dicha prueba: la población de
adultos, las variedades, semanas del año y las parcelas y así mismo, se le
aplico a los resultados obtenidos la prueba de media dentro del mismo programa
para las mismas fuentes, con probabilidad (p ≤ 0,05).
Los conteos se efectuaron durante el
período seco con temperaturas máximas (33,9ºC),
medias (28,1ºC) y mínimas (22,8ºC)
y el período de lluvia presentó temperaturas máximas de (31,9ºC),
medias (27,2ºC) y mínimas (20,4ºC)
y una precipitación total de 1316 mm. (Vivas 2008).
Dichos conteos, se realizaron por un máximo de 18 semanas, desde el inicio de
cada siembra, realizada en enero de los años considerados, hasta la cosecha
entre los meses de abril a mayo (periodo seco) u octubre a noviembre (período
de precipitaciones). Se hizo hincapié en las ultimas 4
a 5 semanas (fase de maduración). Una vez
obtenida la información y después de la observación y procesamiento de los
datos, se procedió al análisis estadístico, empleando diferentes metodologías
para determinar la dispersión espacial: distribución binomial negativa, índice
de Morisita, Ley de potencia de Taylor e índice de Iwao citados por Clavijo 1993; Landeros et al 2003; Rabinovich
1980; Taylor 1984; Trumper et al 2006. También se siguió el procedimiento sugerido por Cochran (1963, 1976, 1977) y Southwood
(1978), señalado por Clavijo (1978a); Vivas (1997a) y Vivas et al.,
(2001). Así mismo se utilizaron los
programas computacionales Statixtic (1990); InfoStat (2004) y “Padis for Windows 95 versión 1.01 y el programa Excel 2000 (Microsoft Office
1997-2000) para el desarrollo de las fórmulas implícitas en el cálculo de los
diversos índices. Del mismo modo, se realizaron las pruebas de medias y test de
significancía para cada uno de los índices
mencionados.
1. Índices de Agregación
Se han desarrollado diferentes clases de índices
con el fin de estimar el tipo de distribución espacial de las poblaciones. De
esta manera, Southwood (1978) propone utilizar la
relación entre la S2 y la :
Donde:
s2/ = relación entre la varianza y la media
Si los valores de la relación, se
aproximan a 1, se puede decir que la distribución de la población es
completamente aleatorizada; valores de 0 o cercanos a este indican una
distribución espacial uniforme y valores mayores de 1 nos señalan una
distribución agregada (Southwood citado por Clavijo, 1978a y Vivas, 1997a y Vivas et al., 2001).
El índice de dispersión se utiliza para
probar la hipótesis nula de que la distribución es al azar, representada
fundamentalmente por la distribución Poisson,
mediante una prueba de Chi-cuadrado (χ2).
De esta manera, la distribución será al azar si el valor del ID está dentro de
los límites (entre las probabilidades 0,95 y 0,05) de los valores de la
distribución χ2 encontrados en las
tablas para n-1 grados de libertad. (Clavijo, 1978 a).
Otro índice muy usado es el cálculo del
parámetro K de la binomial negativa, el cual es calificado como un índice de
agregación de una población y que tiene como limitante la variación de su valor
numérico, producto de las alteraciones en la densidad de la población bajo
estudio (Taylor 1984).
Bliss y Fisher citados por Poole
(1974) señalan tres formas para calcular K y que se determinan por diversas
fórmulas matemáticas.
2. Estimación del parámetro K de la binomial negativa a partir de la
media y la varianza
Los tres métodos para calcular K son:
Método
1:
![]()
La estimación de K por el primer método
está dada por Anscombe citado por Rabinovich
(1980):
Donde:
K1 = Índice de agregación
= Media
S2 = Varianza
Cuando las medias son muy bajas este
método no es confiable, a menos que haya un apreciable grado de agregación (es decir, valores de K menores que 3). Este
método posee una eficiencia del 90% o mas,
bajo las siguientes condiciones:
a) Cuando
la media es pequeña, si la relación K/ > 6;
b)
Cuando es
intermedia, si,
![]()
c)
Cuando es
grande, si K > 13
En caso de dudas en cuanto a la aplicación de esta fórmula,
sobre todo en lo relativo a la calificación de la media (pequeña, intermedia o
grande), se recomienda usar la siguiente ecuación para el cálculo de K:
Método
2:
![]()
![]()
Donde:
N = Número de muestras
f0 = Número de
muestras sin individuos
log = logaritmo en base 10.
Si se conocen N, f0,
y la media, el valor de K2 es aquel valor
que satisface la igualdad, y que solo se puede obtener por prueba y error.
Generalmente, se comienza con un primer valor de K2
que se obtiene interpolando entre dos valores, uno ligeramente mayor y otro
menor que log (N/f0) con este valor de K2, se evalúa {K2
log [1 + (/K2)]} y si esté es diferente de log (N/f0) en más
de un factor preestablecido (por ejemplo 0,01) se incrementa o se reduce
el nuevo valor de K2 a probar, según la
dirección en que se produce la diferencia. (Rabinovich, 1980,
Clavijo, 1993)
Este método es eficiente en 90%, solo
cuando el arreglo tiene una media baja; en casos de medias altas, el método
sigue siendo eficiente solo si, existe un alto grado de agregación. Esto
significa que el método es eficiente en un 90%, si aproximadamente un tercio de
las muestras no poseen individuos cuando la media de la población es menor que
10 individuos por muestra [Southwood citado por Rabinovich (1980)].
Método
3:
Estimación de K por el método de máxima
probabilidad.
En arreglos que puedan ser descritos por
la distribución binomial negativa, pero el parámetro K no puede ser estimado
adecuadamente, por alguno de los métodos descritos anteriormente. En estos
casos, el método de máxima verosimilitud (Haldeane, Sichel, Bliss y Fischer) citados
por Rabinovich (1980), aunque más laborioso, permite
obtener una estimación mucho más eficiente.
![]()
En la expresión ln
= loge, (logaritmo en base e); N es el
total de muestras, es el
estimador de la media, y A(x) es la suma de todas las frecuencias de las
muestras conteniendo más de x individuos [por ejemplo, si una tabla de
frecuencias tiene 6 clases (x = 0, 1, 2, 3, 4, 5) entonces A (0) = F (1) + F
(2) + F (3) + F (4) + F (5), y A(1) = F
(2) + F (3) + F (4) + F (5), etc. ]. La ecuación permite obtener un valor
numérico para K3 (el estimador de K para
el tercer método) si el total de clases en la tabla de frecuencias no excede
20.
De la misma manera, el valor numérico de K3 se logra por prueba y error, se comienza por
un primer valor que puede ser K1 o K2 y modificándose este valor hasta que un
cierto valor de K3 satisfaga la igualdad
dentro de un error preestablecido (por ejemplo 0,01). Si el lado izquierdo de
la igualdad es mayor que el lado
derecho, entonces se debe probar con un K3
ligeramente menor, y a la inversa, si el
lado derecho de la igualdad es mayor que el lado izquierdo.
El valor de K puede ubicarse entre cero e infinito y
cuando se aproxima a infinito la distribución tiende a ajustarse a Poisson (al azar), mientras que cuanto más se acerca a cero
mayor será el grado de agregación de la población y mejor su ajuste a la
binomial negativa. Según Poole (1974) valores
de K hasta un máximo de 8 indican agregación en la población.
Morisita (1962) tratando de evitar el efecto del tamaño de las
muestras en la estimación del nivel de agregación de las poblaciones, menciona
un índice de agregación que asume para ser válido, el que la población este constituida por grupos de individuos espacialmente
diferenciados y que dentro de cada uno de estos grupos la ubicación de los
individuos es al azar. El índice de Morisita se
calcula mediante la fórmula:
![]()
Donde:
Is = Índice de agregación.
ni = Número de individuos en cada una de las muestras.
n = Total de individuos en el total de
muestras.
N = Número de muestras.
Si el índice de agregación es
igual a 1, la distribución es al azar, si es mayor que 1, agregada, y si es
menor que 1 será uniforme.
La significación estadística de la
desviación del índice con respecto a la unidad puede ser probada mediante una
prueba de F, en la cual:
![]()
El valor de Fc es comparado
con la tabla de F con N-1 grados de libertad para el numerador e infinito para
el denominador.
Taylor (1971), para el establecimiento de
la distribución espacial, sugiere una relación empírica entre y s2 de una
población, la cual ha pasado a conocerse como la ley de potencia de
Taylor (Southwood, 1978; Ruesink,
1980; Ruesink y Kogan, 1982
y Clavijo, 1993).
![]()
La relación puede expresarse como:
Donde:
S2 = Varianza
= Media
a = Coeficiente que varía según la
técnica de muestreo
b = Exponente que representa una
constante de las especies.
Al tomar los logaritmos en ambos miembros
se obtiene la ecuación lineal Log S2 = Log
a + b Log . Esta
versión linealizada
permite cuantificar el grado de agregación mediante la pendiente del modelo:
b < 1, b = 1 y b > 1 indican patrones uniforme, aleatorio y agregado
respectivamente. Asimismo, cuanto mayor es el valor de b, mayor es el grado de
agregación (Trumper, 2004).
Cuando a y b son iguales a 1, la relación describe la
distribución de Poisson y estaremos en presencia de
una población con una distribución espacial al azar.(Clavijo,
1993). Pueden darse casos en que b < 1 pero la población es agregada, o b > 1 y la población es uniforme, dependiendo del valor de
a. Además, la agregación de una población varía con la densidad – a muy bajas
densidades una población es uniforme, a medida que la densidad incrementa pasa
por un punto en que es al azar, y luego la distribución se vuelve más agregada.
Otra cosa que hay que considerar es que al usar log para linearizar
la ecuación de Taylor se sobreestima la varianza a densidades bajas. La linearización era común cuando no se tenía el poder
computacional que tenemos ahora, de ser posible hay que calcular a y b usando
regresión no-lineal).
Cuando se utiliza
la ley de potencia de Taylor, “a” representa el intercepto y “b” la pendiente.
Ruesink (1980) indica que para el caso de insectos plaga, el
valor de la pendiente se ubica usualmente entre 1,4 y 2.
Para poder
aplicar estos análisis, se necesita implementar un programa de muestreo con una
plaga dada a lo largo de varias campañas agrícolas. Estos muestreos deben
mantener constante la técnica de muestreo, se deben aplicar siempre en el mismo
cultivo y el tamaño de la unidad muestral debe ser
siempre igual. En efecto, si se comienza el proceso usando una red entomológica
y cada unidad muestral está representada por 5 golpes
de red, entonces se deberá mantener esa
técnica y los 5 golpes como unidad muestral a lo largo de todos los muestreos (Trumper, 2004).
Lloyd
(1967) propone el concepto de agregación media (mean crowding),
refiriéndose al número medio de individuos en relación a un individuo que no
está incluido en dicha media, cuando todos están ubicados en una misma área. La
intención de la medida es la de indicar los posibles efectos de interferencia o
competencia que pudiesen derivarse de un encuentro al azar. Tiene validez
si se aplica sobre individuos que se mueven libremente en un hábitat continuo y
uniforme, sin mostrar territorialidad. La agregación media se calcula de la siguiente forma:
![]()
Donde:
![]() = Agregación media
= Agregación media
S2 = Varianza
= Media
Utilizando
la agregación media (![]() ) en relación a la media de la densidad de la población (), Lloyd (1967) calcula el grado de agregación de la
misma en función de un índice de parche (patchiness)
que se calcula con la fórmula:
) en relación a la media de la densidad de la población (), Lloyd (1967) calcula el grado de agregación de la
misma en función de un índice de parche (patchiness)
que se calcula con la fórmula:
![]()
Donde K representa el parámetro de la
binomial negativa, pudiendo ser tomado como una medida de agregación
independiente del tipo de distribución considerada.
Si la relación entre la
agregación media y la media de la densidad de la población es < 1, su distribución
será uniforme. Si = 1, la distribución será al azar y si la relación es > 1,
la distribución será agregada.
Iwao (1971), señala que lo propuesto por Lloyd es una
buena medida de la agregación de la población cuando existe un sólo tipo de
distribución espacial, mientras que si existe más de un tipo de distribución,
la regresión entre la agregación media como variable dependiente y la media de
la densidad de la población como variable independiente, rinde mejor
información biológica. El uso de la regresión propuesta por Iwao elimina el problema que ocurre en el cálculo de otros
índices cuando ocurren cambios en la densidad de la población, permitiendo así
la estimación del tamaño de la muestra y la escogencia de la transformación
adecuada de los datos para el análisis de la varianza (Iwao
y Kuno, 1968).
Los diversos métodos propuestos para la determinación
del patrón de distribución espacial, refuerzan la importancia de este aspecto
como atributo específico y obligan a tener cuidado en su estimación porque no
sólo cambia entre especies sino que la misma puede variar según las
circunstancias.
Modelos utilizados para determinar la
dispersión espacial: Morisita; Ley de potencia de
Taylor e Iwao (Clavijo, 1993; Cabrera et al., 2002; Landeros et al, 2003; Rabinovich, 1980; Taylor, 1984; Trumper et al, 2006). Las
fórmulas para dichos índices se describen en el cuadro 1 con sus respectivos
valores para las diferentes distribuciones.
|
Cuadro 1. Fórmulas para los índices con sus
respectivos valores para las diferentes distribuciones utilizadas en el
estudio de Oebalus insularis en tres parcelas del sistema
de riego río Guárico en Calabozo, estado Guárico, Venezuela. |
||||
|
Índice |
Fórmula |
Distribución Uniforme |
Distribución al Azar |
Distribución Agregada |
|
Morisita |
|
< 1 |
= 1 |
> 1 |
|
Ley de potencia de Taylor |
(Log
S2 = Log a + b log ) |
b
< 1 |
B
= 1 |
b
> 1 |
|
Iwao |
α + β |
β < 1 |
β = 1 |
β > 1 |
El índice de Iwao presenta
los siguientes símbolos
“α”, “β” y “”, por medio
de esté índice se analiza la distribución espacial realizando una
regresión lineal donde “” es la densidad media de la muestra y dentro de la
regresión correspondiente al eje de la ordenada de X, “α” es un factor de muestreo
determinado por la línea de regresión.
Cabrera et al.,
(2002) definen a “α” como el índice básico de
contagio y representa
por cada individuo
en la muestra,
cuantos se espera que convivan con él, β es el coeficiente de
densidad de contagio el cual define la manera en que los individuos se
dispersan por si mismos dentro del hábitat. Si α < 0, los individuos tienden a la repulsión; si α = 0, los individuos tienden a estar aislados y si α > 0, los
individuos tienden a agruparse o a formar colonias. Si β < 1, los individuos o colonias se distribuyen
regularmente; si β = 1, la disposición será al azar y si β > 1, la disposición será agregada. Se utilizó el
programa “Padis” for Windows 95 versión
1.01, para verificar la significación de los parámetros α y β.
3. Cálculo de la bondad de ajuste
La
bondad de ajuste a la binomial negativa se prueba mediante el calculo de los estadísticos U o T y el de sus respectivos
errores estándar (Clavijo 1993). El uso de U o T, así como el valor aproximado
de sus errores estándar puede lograrse utilizando un gráfico denominado:
Errores standards aproximados de T y U para N =
100 (Clavijo, 1993), recomendándose U si las X son pequeñas y T si son grandes.
Si se utiliza U su estimación
se hará mediante la fórmula siguiente:
![]()
La
varianza de U se calcula por medio de la fórmula citada por Poole
(1974). Calculado el valor de U o T, y
estimando los errores estándar mediante el grafico 19 en Evans citado por
Clavijo (1993) y Poole (1974), se dirá que hay un
buen ajuste a la binomial negativa si el rango de valores, producto de sumar y
restar los errores estándar a sus respectivos estadísticos (U o T) incluye el
valor (0); de ser el caso, la población
bajo estudio muestra una distribución espacial agregada.
El parámetro K es una de las hipótesis
fundamentales en el uso de la estadística secuencial. Sí el valor de K, se
incrementa con la media de la muestra, se puede calcular un K común, denotado
como Kc, (Bliss y Owen 1958). Osager citado por Clavijo (1993). Estos valores se
utilizaron para la determinación del plan de muestreo secuencial de la chinche vaneadora del grano de arroz (Vivas, 2008; Vivas y Notz, 2009).
En el cálculo del parámetro k, se utilizó el paquete
computacional “Padis for
Windows 95 versión 1.01, propuesto por
López y Osada (1997). Los
índices seleccionados en este trabajo fueron: el índice de Morissita; la ley de potencia de Taylor, el índice de Iwao, la relación
s2/, y el modelo matemático de la binomial
negativa.
RESULTADOS Y DISCUSIÓN
Al
emplear el análisis estadístico de Kruskal-Wallis a
la información proveniente de las poblaciones de adultos en las tres parcelas
del sistema de riego río Guárico (SRRG) y los cuatro
años de estudio; se obtuvo la información que se presenta en el Cuadro 2. No se
observaron diferencias significativas entre las poblaciones de adultos de la
chinche para las parcelas bajo estudio y durante los cuatro años, por lo tanto, esto permitió que se combinara
la información de las tres parcelas en cada año (Cuadro 2).
|
Cuadro 2. Análisis estadístico de la población de adultos de Oebalus insularis en
tres parcelas del sistema de riego río Guárico en Calabozo, estado Guárico,
Venezuela. |
||||
|
Parcela † |
Medias (2001) |
Medias (2002) |
Medias (2003) |
Medias (2004) |
|
152 |
390,31 a |
380,33 a |
402,11 a |
396,51 a |
|
173 |
400,61 a |
410,41 a |
409,41 a |
407,65 a |
|
Lote INIA Guárico |
426,59 a |
407,63 a |
415,91 a |
419,33 a |
|
† Prueba de Kruskal-Wallis. Valores seguidos de una misma letra en la
columna, no son significativamente diferentes al nivel de 5%. En paréntesis
el año bajo estudio. |
||||
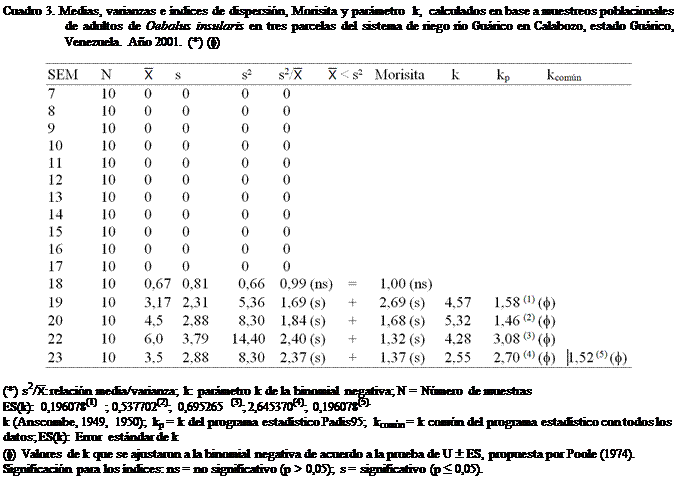
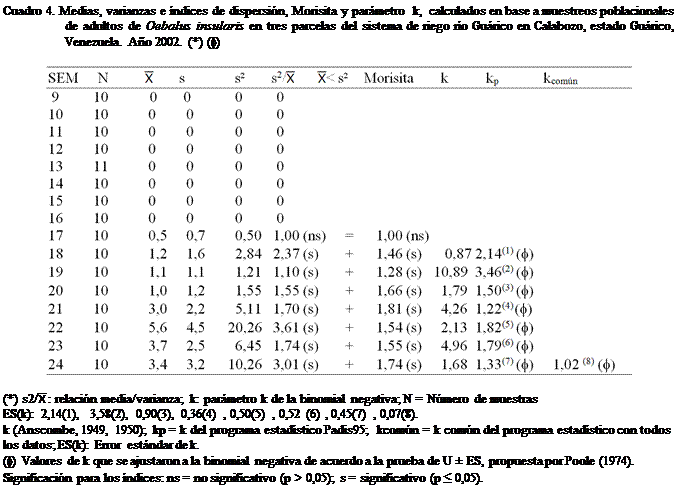
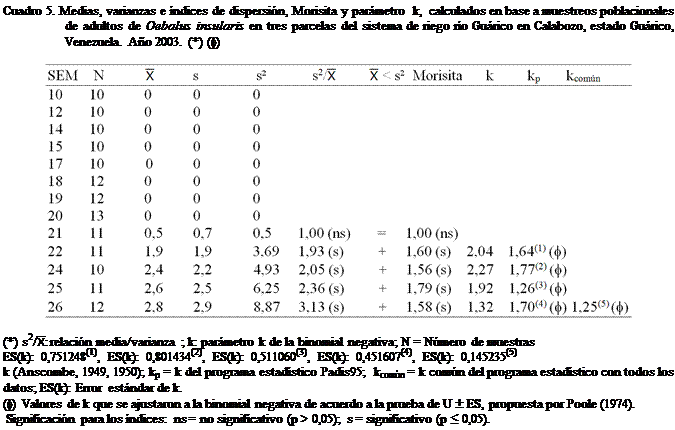
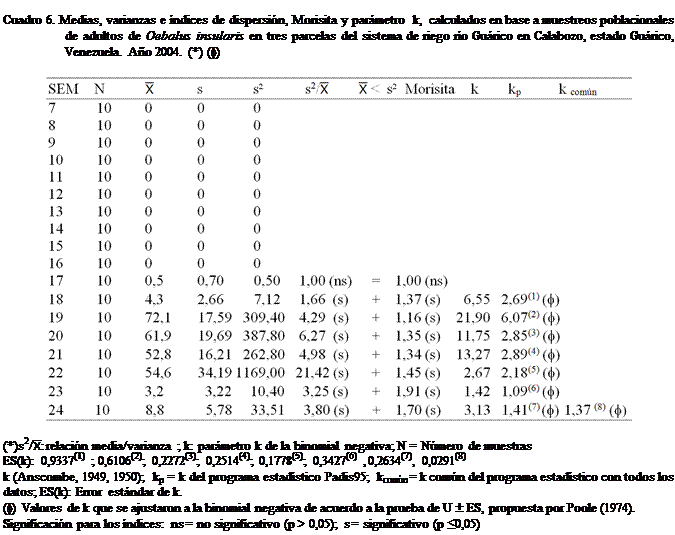
Al aplicar los criterios de Soutwood
(1966) a los datos obtenidos en este trabajo (Cuadros 3, 4, 5 y 6), se observó
que la mayoría de las poblaciones estimadas de adultos de O. insularis en las tres parcelas del SRRG; al tomar en consideración la semana del año,
presentaron según la relación (s2/): medias inferiores a las
varianzas, lo que permite decir, en una primera instancia que la distribución
en el campo sigue un patrón agregado.
Además, las mayores poblaciones del adulto de
la chinche vaneadora se observaron durante la época
de lluvias que coincide con las semanas 19 a 25 del año (mayo a julio) y con la
fase de maduración del grano de arroz; información que coincide con la obtenida
por Aponte et al. (1992, 1997); Vivas
(1997b; 2008) y Vivas et al. 2010) en los estados Portuguesa y Guárico e igualmente, con
lo observado por Daza (1991); Gómez y Meneses (1985); Red de mejoramiento de
arroz para el Caribe (1991); Pantoja et
al. (1997) y Weber (1989).
En los
Cuadro 4 y 6, se puede observar que de un total de ocho estimaciones de
población realizadas en las parcelas,
siete (87,5%) presentaron una distribución agregada, mientras que el resto 1
(12,5%), presentó una distribución al azar. Lo antes indicado corrobora que las
poblaciones de O. insularis se distribuyen de manera
agregada. En los cuadros 3 y 5, se observan iguales resultados, pero en menor
número de estimaciones.
En los mismos cuadros 3, 4, 5 y 6, se
presenta el tipo de distribución que presentó O. insularis
en el área de estudio. Los índices citados (s2/, Morisita y el parámetro k)
muestran una disposición espacial de la población de forma agregada; pudiéndose
afirmar lo antes expuesto. Cabe mencionar que en las parcelas, cuando las
poblaciones resultaron bajas, la distribución fue al azar. Esto pudo deberse a
que el método de evaluación no resultó el más idóneo que según Taylor, citado
por Clavijo (1993) demuestra la incapacidad del método para estimar la
verdadera distribución o que sea
necesario tomar un mayor número de muestras para detectar la distribución real
(Kogan y Herzog, 1980;
Taylor, 1984; Gómez e Higuera, 1986).
En el Cuadro 7, se presenta la información del calculó
de k común con todos los datos por año.
|
Cuadro 7. Cálculo del
parámetro k común para los años en estudio de Oebalus
insularis en
tres parcelas del sistema de riego río Guárico en Calabozo, estado Guárico,
Venezuela † |
|||||
|
Año |
2001 |
2002 |
2003 |
2004 |
k común del set de datos |
|
k común |
1,525 |
1,025 |
1,258 |
1,375 |
1,381 |
|
ES (k) |
0,196 |
0,077 |
0,145 |
0,029 |
0,029 |
|
† k: parámetro k de la
binomial negativa; ES (k): Error
estándar de k; Programa Padis for
Windows 95 |
|||||
Como se observa el k para O. insularis, se encontró entre 1,025 y 1,525 y para
efectos de los cálculos en este trabajo, se utilizó como valor de k = 1,381 con un error estándar (k) de 0,029
(Cuadro 7).
La bondad de ajuste de la distribución binomial
negativa para la distribución de las frecuencias observadas se analizó mediante
el cálculo del estadístico U. Se obtuvo para cada año y para el k común, los
respectivos valores de U, Var (U) y su error estándar (ES), cumpliéndose para
cada caso la relación: U ± ES, propuesta por Poole (1974).
El valor estimado de U más su error estándar (ES)
contiene el valor cero (0), para cada uno de los valores del parámetro (k)
obtenido en cada año e igualmente, para el k común; lo que permite concluir que
la binomial negativa se ajustó a la distribución de las frecuencias
observadas.
De una manera general, el valor de k es indicativo del
valor de la agregación de la población y
puede ubicarse entre 0 e infinito. Cuando k se aproxima a infinito la
distribución tiende ajustarse a Poisson (al azar),
como ocurrió cuando las poblaciones resultaron muy bajas (Cuadros 3, 4 y 5)
mientras que cuanto más se acerca a cero mayor será el grado de agregación de
la población y mejor su ajuste a la binomial negativa (Clavijo 1993; Poole (1974).
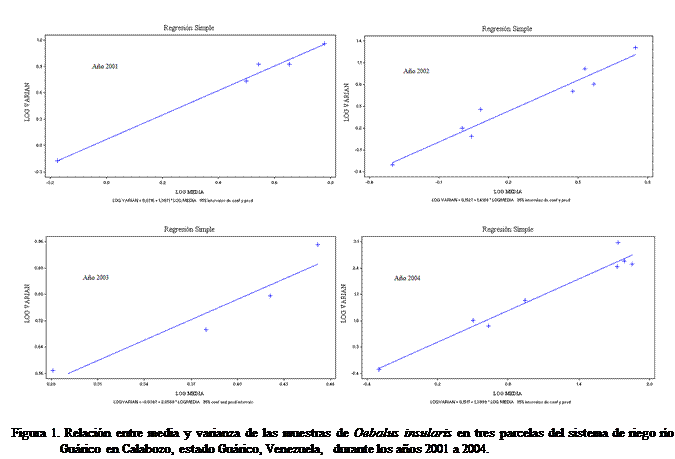
En el Cuadro 8, aplicando la Ley de Potenciación de
Taylor, es decir la regresión del Log10 de
la media sobre el Log10 de la varianza, se
obtuvieron pendientes (b) positivas y significativamente mayor que uno, (b
entre 1,387 y 2,058) con una (p > 0,0001); lo cual también indica una distribución del tipo
agregada.
|
Cuadro 8.
Cálculo de los parámetros y análisis de regresión empleando la ley de
potenciación de Taylor durante los
años de estudio de Oebalus insularis
en tres parcelas del sistema de riego río Guárico en Calabozo, estado
Guárico, Venezuela. |
|||||
|
Año |
Regresión |
R2 |
Probabilidad |
log a* |
b* |
|
2001 |
Y = 0,07164 + 1,38715 X |
0,9832 |
p ≤ 0,001 |
0,07164 |
1,3871 |
|
2002 |
Y = 0,15274 + 1,41881 X |
0,9339 |
p ≤ 0,000 |
0,15274 |
1,4188 |
|
2003 |
Y = -0,03866 + 2,0588 X |
0,9018 |
p ≤ 0,050 |
0,03866 |
2,0588 |
|
2004 |
Y = 0,15168 + 1,39992 X |
0,9493 |
p ≥ 0,000 |
0,15168 |
1,3999 |
|
(*) a: antilogaritmo de la intersección con la ordenada; b:
pendiente de la línea de regresión; R2: coeficiente de determinación. |
|||||
En la Figura 1,
se observa el buen ajuste de las observaciones a la línea de regresión que
corrobora los altos valores obtenidos con los coeficientes de determinación.
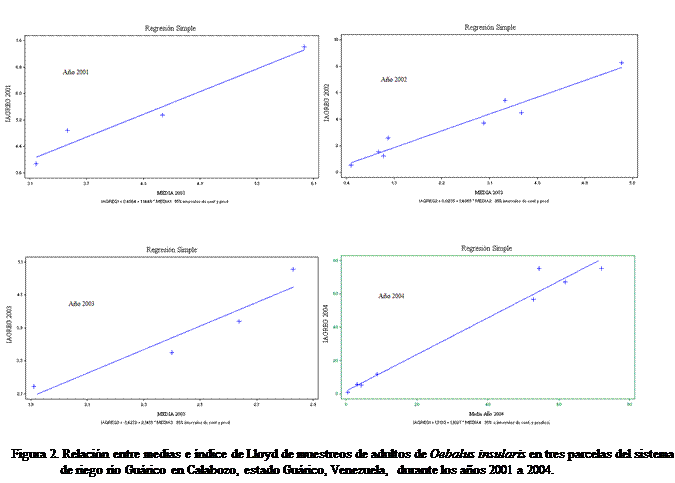
La regresión del índice de agrupamiento medio de Lloyd
sobre el número medio de adultos de O. insularis
por muestra, produjo el índice de agregación de Iwao
que se describe en el Cuadro 9, en la cual se detalla la línea de regresión, el
coeficiente r, la probabilidad y los parámetros alfa y beta.
|
Cuadro
9. Cálculo de los coeficientes y análisis de regresión empleando el modelo de
Iwao durante los años de estudio de Oebalus insularis
en tres parcelas del sistema de riego río Guárico en Calabozo, estado
Guárico, Venezuela. (+) |
|||||
|
Año |
Regresión |
R2 |
Probabilidad |
α |
β |
|
2001 |
Y= 0,45637 + 1,14463
X |
0,9562 |
p ≤ 0,0222 |
0,45637 |
1,14463 |
|
2002 |
Y= 0,02353 + 1,40646
X |
0,9493 |
p ≤ 0,0000 |
0,02353 |
1,40646 |
|
2003 |
Y= -1,42716 + 2,14550
X |
0,9010 |
p ≤ 0,0340 |
1,42716 |
2,14550 |
|
2004 |
Y= 1,51926 + 1,10270
X |
0,9722 |
p ≤ 0,0000 |
1,51926 |
1,10270 |
|
(+) α = Índice básico de contagio (Intercepto de Y) β = (Pendiente) Coeficiente de densidad
de agregación ; R2:
coeficiente de determinación. |
|||||
Alpha (α) se define como el índice básico de agregación que representa cada individuo en la muestra y
cuantos se espera que convivan con él, y β es el
coeficiente de densidad de agregación. El
modelo en todos los casos resultó estadísticamente significativo con valores de
(p ≤
0,0001); alcanzándose un buen ajuste a
las observaciones (Figura 2) tal como se observó para el caso de la ley de
Taylor. El parámetro β presentó valores mayores a 1 (entre 1,10 y 2,14) para los adultos (p ≤ 0,01), demostrando que se distribuye en el campo de
una forma agregada. De la misma manera, cuando se considera el parámetro α ó índice básico de agregación (Cabrera et al., 2002), puesto que dicho parámetro presentó valores mayores
que cero (α > 0) (p > 0,05); los individuos tienden a agruparse o formar
colonias y en todos los casos estudiados se cumplió con esta condición.
Resultados similares a los obtenidos
en este trabajo han sido reportados, para la misma especie y en el estado
adulto, por la Red de Mejoramiento de Arroz para el Caribe (1991) en Cuba, y,
para una especie similar, O. pugnax,
por Foster et al. (1989) en Florida y Espino et al. (2008) en el sureste de Texas; mientras que Daza (1991) en
Colombia, menciona que no existen patrones de agregación de las especies O. insularis y O. ornatus
dentro del campo y las mayores poblaciones se encuentran durante el período de
maduración del cultivo.
Por otro lado, conclusiones muy similares
en cuanto a la disposición espacial que muestran agregación se consiguen en
otras plagas y cultivos. Así se puede citar el caso del ácaro Phyllocoptruta oleivora
en cítricos en donde se probaron
doce índices de dispersión y la mayoría mostró agregación (Badii
et al. citado por Landeros et al. 2003). Igualmente, Trumper et al.
(2006) demostraron que los desoves de Diatraea
saccharalis evidencian un patrón de distribución
agregado empleando la ley de Taylor en el cultivo del maíz.
De la misma manera, Cabrera et al. (2002) empleó diferentes
criterios de ajuste y significación estadística para calcular los estimadores
de la ley de potencia de Taylor y la regresión de Iwao
como indicadores ecológicos del patrón espacial de poblaciones de Thrips palmi Karny, muestreadas en plantaciones de papa, Solanum tuberosum
L. Ellos encontraron el mejor ajuste con la ley de potencia de Taylor pero en
ambos casos apreciaron que tanto las larvas como los adultos se distribuyeron
en forma agregada, mientras que López (1994) trabajando con larvas de Anopheles nuneztovari
(Gabaldon) también obtiene resultados similares, al
igual que Notz (1992) en estudios con las
especies Scrobipalpula
absoluta (Meyrick) y Phthorimaea
operculella Zeller (Lepidoptera: Gelenchiidae) en el
cultivo de la papa.
Igualmente, Vivas (1997a),
trabajando con el saltahojas T. orizicolus, encontró que la población de adultos se
distribuyó en forma agregada y Rashid et al., (2006) menciona que Oebalus pugnax en arroz en
USA, se distribuye de manera agregada en campo
La explicación biológica que determinó
que la distribución de los adultos de O. insularis fuera agregada, se deba a la concentración
de individuos por panícula, él cual es corroborado por el coeficiente
α, obtenido en el análisis de regresión de Iwao.
CONCLUSIONES
La población de adultos de la chinche vaneadora del grano
de arroz presentó un patrón de distribución
en el campo del tipo agregada
AGRADECIMIENTO
A Henry González y Dilcia
Astudillo por su colaboración en la toma de muestras y a Zurhilma
Narváez por las sugerencias en el trabajo.
LITARATURA CITADA
Adams, M.; R. Vargas y
A. Montaldo. 1990. El arroz en Venezuela. Rev. Fac. Agron. Maracay. UCV. Facultad de Agronomía, Comisión de Información,
Documentación y Publicaciones. Alcance N° 39. 263 p.
Andrews, K. L y J. R.
Quezada. 1989. Manejo integrado de plagas insectiles en la agricultura: Estado
actual y futuro. Departamento de protección Vegetal. Escuela de Agricultura
Panamericana. El Zamorano, Honduras, Centro América. 587 p.
Aponte, O.; L. E. Vivas, L. E.
Escalona, L. M. Ramírez y F. P. Freitez. 1992. Manejo
integrado de artrópodos plaga en el cultivo de arroz en Venezuela. Unidades de
aprendizaje para la capacitación en tecnología de producción de arroz. CIAT - BID - FONAIAP - APROSELLO - APROSELLAC - UNELLEZ. 144 p.
Aponte, O.; L. E. Vivas, L. E. Escalona y P. Castillo. 1997.
Manejo integrado de artrópodos plaga en
arroz. Unidad de Aprendizaje para la Capacitación Tecnológica en la
producción de arroz. FONAIAP – FUNDARROZ - UCV - IUTEP. Acarigua,
Venezuela. 59 p.
Bliss C.
I. and A. R. G. Owen. 1958. Negative binomial distributions with a common K. Biometrika 45: 37-58.
Cabrera A.;
W. Guerra y M. Surís. 2002. Selección de modelos de
regresión para describir el patrón espacial de Trips
palmi Karny (Thysanoptera: Thripidae) en el
cultivo de papa. Cultivos Tropicales 23 (4): 76-81.
Clavijo,
S. A. 1978. Distribución espacial del gusano cogollero del maíz Spodoptera frugiperda (Smith)
(Lepidoptera : Noctuidae). Rev. Fac. Agron. (Maracay) Alcance 26:
93-99.
Clavijo,
S. A 1993. Fundamentos de manejo de plagas. Universidad Central de Venezuela.
Facultad de Agronomía. Consejo de Desarrollo Científico y Humanístico. Caracas,
Venezuela. 205 p.
Cochran,
W. G. 1977. Sampling techniques. Third ed.
John Willey and Sons. Inc, Toronto. Canada. 428 p.
Cheaney, R. L. y P. R. Jennings. 1975.
Problemas en cultivos de arroz en América Latina. Cali, Colombia; Centro
Internacional de Agricultura Tropical. p. 30-34.
Chacín, F. L. 1999. Avances
recientes en el diseño y análisis de experimentos. Universidad Central de
Venezuela. Facultad de Agronomía. Maracay, Venezuela. 257 p.
Daza, C. E. 1991. Biología,
daño y enemigos naturales de hemípteros pentatómidos
presentes en el cultivo de arroz con riego. Tesis de Grado. Universidad
Nacional de Colombia. Facultad de Ciencias Agropecuarias. Palmira, Colombia. 65
p.
De Galvis Y.
C.; J. González y J. Reyes. 1982. Descripción y daño de los insectos que atacan
el arroz en América Latina. Guía de estudio. Cali, Colombia: Centro
Internacional de Agricultura Tropical (CIAT) . 36 p.
Drees, B. M. 1996. Texas
rice production guidelines. Texas Agr.
Ext. Service. The Texas A and M University System. 5 p.
Espino L,; M. O. Way and L. T. Wilson L. T. 2008. Determination of Oebalus pugnax (Hemiptera: Pentatomidae) spatial
pattern in rice and development of visual sampling methods and population
sampling plans. J. Econ. Entomol. 101 (1): 216-25.
Food and Agriculture Organization (FAO). 2006. Seguimiento del mercado del
arroz. Roma, IT, FAO. Documento en línea Disponible
en: ftp://ftp.fao.org/docrep/fao/009/ag068s/ag068s00.pdf. Fecha de consulta: 08-10-2008.
Foster, R. E.; R. H. Cherry and D. B. Jones. 1989. Spatial distribution
of the rice stink bug (Heteroptera: Pentatomidae) in Florida rice. J. Econ. Entomol. 82 (2): 507-509.
García, J. L. 1982.
Estudio sobre la biología, comportamiento y ecología de Spodoptera
frugiperda (Smith) (Lepidoptera:
Noctuidae). Tesis Doctoral. Facultad de Agronomía.
Universidad Central de Venezuela. 222 p.
Gómez, A. D.
y A. M. Higuera. 1986. Bases para el manejo integrado de plagas. Revisión
crítica de la investigación entomológica. Fondo Nacional de Investigaciones
Agropecuarias (FONAIAP), Estación Experimental Zulia.
Serie D N° 1-21. Maracaibo, Venezuela. 92 p.
Gómez, J. y R. Meneses.
1980. Dinámica poblacional de Oebalus insularis (Stal.) (Hemiptera: Pentatomidae) en la
zona arrocera de Sancti Spíritus, Cuba. Centro Agrícola 7 (2): 41-48.
Gómez, J. y R. Meneses.
1985 Biología de Oebalus insularis, (Heteroptera: Pentatomidae) sobre Echinochloa colonum.
Ciencia y Técnica en la Agricultura. Arroz 8 (2):
29-38.
Gramene. 2006. Gramene
species: cereal statistic.
Documento en línea. (en línea). Disponible en: http://www.gramene.org/species/cereals.html. Fecha de
consulta: 10-10-2008
Guharay, F. 2002. Biología, daño y manejo de Oebalus insularis,
la chinche de la espiga del arroz. Revista Manejo Integrado de plagas. Hoja
técnica, publicaciones periódicas. CATIE, Costa Rica.
51. P.
Gutiérrez, A.; E.
Arias, A. García y R. Corona. 1985. Evaluación del nivel de daño causado por
diferentes índices de población de Oebalus insularis en el cultivo de arroz. Ciencia y Técnica en
la Agricultura. Arroz 8 (1): 63-74.
Gutiérrez, A.; R.
Meneses, E. Arias, A. García y A. Hernández. 1987. Estimación de las
poblaciones de Oebalus insularis en el cultivo del arroz.
Ciencia y Técnica en la Agricultura. Arroz 10 (1): 43-53.
Gutiérrez, A.; R.
Meneses, A. Arias, A. Hernández y M. Amador. 1991. La chinche del arroz en
Cuba. Arroz en las Américas. Boletín del Programa Arroz del CIAT
12 (2): 2-4.
Gutiérrez, A.; R.
Meneses y R. Corona. 1982. Pérdidas ocasionadas por la alimentación de Oebalus insularis en
la fase lechosa del grano de arroz. Ciencia y Técnica en la Agricultura. Arroz
5 (1): 71-79.
Infostat. 2004. InfoStat versión
2004. Grupo InfoStat, Facultad de Ciencias ASgropecuarias. Universidad Nacional de Córdoba, Argentina. 200 p.
Iwao, S. 1971. An
approach to the analysis of aggregation pattern in biological populations. Spatial patterns and
statistical distributions. The Pennsylvania State
University Press. University Park. London. UK. p. 461-513.
Iwao,
S and E. Kuno. 1968. Use the regression of
mean crowding on mean density for estimating sample size and the transformation
of data for the analysis of variance. Res. Popul.
Ecol. 10: 210-214.
Kogan, M and D. C. Herzog. 1980.
Sampling methods in soybean entomology. Springer-Verlag. New York. USA. 587 p.
Landeros,
J.; J. Baldera, M. H. Badii,
E. G. Sánchez, E. Guerrero y A. E. Flores. 2003. Distribución espacial y
fluctuación poblacional de Phyllocoptruta oleivora (Ashmead) (Acari: Eriophyidae) en cítricos
de Guemez, Tamaulipas. Acta
Zoo. Mexicana (n.s.) 89: 129-138.
López, D. M. 1994. Análisis de la dispersión y la abundancia de los
estados larvales de Anopheles nuneztovari (Gabaldon) en
estanques piscícolas del municipio de Buenaventura, Colombia. Bol. Mus. Ent. Univ. Valle 2 (1-2): 73-84.
López, J. C. y H. K. V. Osada. 1997. Programa computacional “Padis for Windows
95. Version 1.01.
Lloyd, M.1 967. Mean crowding. J. Anim. Ecol. 36: 1-30.
Meneses, R. C.; A. Y.
Gutiérrez, A. R. García, G. P. Antigua y J. S. Gómez. 1995. Guía para el
trabajo de campo en el manejo integrado de plagas del arroz. Instituto de
Investigaciones del Arroz. Estación Experimental del Arroz “Sur del Jibaro”.
Cuba. 26 p.
Meneses R. C.; A. Y.
Gutiérrez, A. R. García, G. P. Antigua, J. S. Gómez, F. Correa Victoria y L.
Calvert. 2001. Guía para el trabajo de campo en el manejo integrado de plagas
del arroz. CIAT, IIA-Cuba, FLAR. Publicación del Fondo Latinoamericano para arroz de
riego (FLAR). Cuarta edición revisada y ampliada.
Cali, Colombia. 76 p.
Morisita, M. 1962. Ig-Index,
a measure of dispersion of individuals. Res. Popul.
Ecol. 5: 1-7.
Narres,
J. S and C. M. Smith. 1984. Feeding preference of the rice stink bug on
annual grasses and sedges. Entomologia Experimentalis et Applicata. 35:
1-17.
Notz, A. P. 1992. Distribución espacial y temporal de Scrobipalpula absoluta (Meyrick)
y Phthorimaea operculella
Zeller (Lepidoptera: Gelenchiidae) en papa, Solanum
tuberosum. Rev. Fac. Agron. (Maracay). 18: 413-424.
Pantoja, A.; A. Fischer, F. Correa
Victoria, L. R. Sanint y A. Ramírez. 1997. MIP en Arroz: Manejo integrado de plagas; artrópodos,
enfermedades y malezas. Calí, Colombia. Centro
Internacional de Agricultura Tropical. Publicación CIAT
N° 292. 141 p.
Poole, R. W. 1974. An introduction to quantitative
ecology. McGraw-Hill. New York. USA. 532 p.
Portal, F. D. C.; D.
Castillo y H. Pampin. 1978. Algunas observaciones
sobre Solubea insularis
(chinche) y sus efectos sobre el grano de arroz. Ciencia y Técnica en la
Agricultura. Arroz 1 (2): 75-76.
Rabinovich, A. 1980. Introducción a la ecología de poblaciones de animales. No
20. Primera edición. Editorial Continental S. A. México. 330 p.
Rashid,
T.; D. T. Johnson and J. L. Bernhardt. 2006. Sampling rice stink bug (Hemiptera: Pentatomidae) in and
around rice fields. Environ. Entomol. 35: 102-111.
Red de
Mejoramiento de Arroz para el Caribe. 1991.
Mesa redonda sobre protección vegetal. J. Armenta Soto y M. Castillo (Eds). Cooperación: CIAT-CIDA-IRRI-IICA-SEA-UNDP. Santo
Domingo, República Dominicana.
107 p.
Ruesink, W. G. 1980. Introduction
to sampling theory. Sampling methods in soybean
entomology. Springer Verlag. New York. USA. p: 61-78.
Ruesink, W. G and M. Kogan. 1982. The quantitative basis of pest
management: sampling and measuring. Introduction to pest
management. John Wiley and Sons. New York, USA.
p. 315-352.
Sánchez, C. E. 1995. El arroz, estrategia agrícola y
alimentaría en Venezuela. III Taller
nacional sobre la importancia del arroz. IUT –
Los llanos. Calabozo. Editorial Corprensa. 275 p.
Segnini, S. 1984. Biología y ecología poblacional de Empoaska
kraemeri Ross y Moore (Homoptera:
Cicadellidae) en caraota (Phaseolus
vulgaris). Tesis Doctoral. Facultad de Agronomía.
Universidad Central de Venezuela. 207 p.
Southwood, T. R. E. 1966. Ecological methods with particular reference to the study of insect
populations. Methuen and Co. LTD London. UK. 383 p.
Southwood, T. R. E. 1978. Ecological methods. Second ed. Chapman and
Hall Co. London, UK. 524. pp.
Statixtix. 1990. Paquete
computacional, Segunda edición. 100 p.
Taylor, L. R. 1971. Aggregation as a species characteristic. Spatial patterns and statistical distributions.
The Pennsylvania State University Press. University
Park. London, UK. p. 357-377.
Taylor, L. R. 1984. Assessing and interpreting
the spatial distributions of insect populations. Ann. Rev. Entomol. 29:
321-357.
Trumper, E. V. 2004. Bases para el diseño de planes de muestreo de plagas. Serie: Modelos bioeconómicos para la toma de decisiones de manejo de
plagas. Estación Experimental Manfredi. Sección
Entomología. Año (I). Nº
2. Disponible en: www.inta.gov.ar/manfredi/info/documentos/docprodveg/entomó/bioeco2.htm. Visitado: 3 de agosto de 2007.
Trumper, E. V.; F. Fava y J. M. Imwinkelried. 2006. Desarrollo
de un plan de muestreo secuencial para la estimación de densidad de desoves de Diatraea saccharalis
con unidades muestrales compuestas. Serie: Modelos bioeconómicos para la toma de decisiones de manejo de
plagas. Estación Experimental Manfredi. Sección
Entomología. Año (III). Nº 1. Disponible en: www.inta.gov.ar/manfredi/ info/documentos/docprodveg/entomó/bioecoIIIS3.htm.
Visitado:
14 de mayo de 2007.
Viator,
H. P.; A. Pantoja and C. M. Smith. 1983. Damage to
wheat seed quality and yield by the rice stink bug and southern green stink bug
(Hemiptera: Pentatomidae). J. Econ. Entomol. 76 (6):
1410-1413.
Vivas,
L. E. 1997a. Dinámica poblacional de la sogata del arroz Tagosodes orizicolus (Homoptera: Delphacidae) en el Guárico Occidental. Tesis de Maestría.
Facultad de Agronomía. Universidad Central de Venezuela. Maracay, Venezuela.
147 p.
Vivas,
L. E. 1997b. El chinche vaneador
del arroz Oebalus ypsilongriseus (Degeer) (Hemiptera: Pentatomidae) en Venezuela. Publicado por Fundacite (Aragua), Disponible en: http://www.plagas-agricolas.info.ve/. 4 p. Visitado: 3 de
junio de 2007.
Vivas L. E. 1999. Manejo de insectos plagas en Calabozo. Boletín
Resiembra. Concepto Milenium. Calabozo, Guárico. 1
(2): 5 p.
Vivas, L. E. 2002. Manual de
insectos plagas de arroz. Primera Edición. INIA-SINGENTA.
Maracay, Venezuela. Comunicación Gráfica C. A. 30 p.
Vivas, L. E. 2008.
Muestreo secuencial del chinche vaneador del arroz, Oebalus insularis Stal (Hemiptera: Pentatomidae) sobre arroz (Oryza
sativa L.) en Calabozo, estado
Guárico. Tesis de Doctorado. Facultad de Agronomía. Universidad Central de
Venezuela. Maracay, Venezuela. 144 p.
Vivas L. E.; S. Clavijo
y H. González. 2001. Distribución temporal y espacial en poblaciones de Sogata Tagosodes orizicolus
(Muir) 1926 (Homoptera:
Delphacidae) y número óptimo de muestras para
su estimación en el cultivo de arroz, en Calabozo, estado Guárico, Venezuela. Investigación Agrícola 6: 1. Disponible en línea:
http://www.redpavfpolar.info.ve/danac/volumen6/art1/index.html. Visitado: 02 de
mayo de 2005.
Vivas L. E.; L. Lugo, M. Acevedo y
S. Clavijo. 2002. Determinación de la preferencia de Tagosodes orizicolus (Muir) 1926 (Homoptera: Delphacidae) sobre
variedades de arroz en Calabozo, estado Guárico, Venezuela, Investigación
Agrícola (7). Disponible en línea: http://www.redpav-fpolar.info.ve/danac/viewarticle.php?id=33.
Visitado: 15-05-2005
Vivas L. E y A. Notz. 2009. Plan de muestreo
secuencial de Oebalus insularis Stal (Hemiptera: Pentatomidae) en el cultivo de arroz en Calabozo estado
Guárico, Venezuela. Revista UDO Agrícola 9 (4): 857-892.
Vivas
L. E.; A. Notz y D. Astudillo. 2010. Fluctuación
poblacional del chinche vaneadora en parcelas de
arroz, Calabozo, Estado Guárico, Venezuela. Agronomía Trop.
60 (1): 61-73.
Weber, G. 1989.
Desarrollo del manejo integrado de plagas del cultivo de arroz: Guía de
estudio. Centro Internacional de Agricultura Tropical (CIAT).
Calí, Colombia. 69 p.
Página
diseñada por Prof. Jesús Rafael Méndez Natera
ÍNDICE
DE LA REVISTA CIENTÍFICA UDO AGRÍCOLA (REGRESO)



