Revista
Científica UDO Agrícola Volumen 10. Número 1. Año 2010. Páginas: 48-54. Nota
Técnica
Evaluación de genotipos de maíz en condiciones
deficientes de humedad en Durango, México
Evaluation of corn genotypes in conditions of scarce soil moisture at
Durango, México
José Dimas LÓPEZ MARTÍNEZ  ,
Armando ESPINOZA BANDA, Enrique SALAZAR SOSA, Ignacio ORONA CASTILLO y Cirilo VÁZQUEZ VÁZQUEZ
,
Armando ESPINOZA BANDA, Enrique SALAZAR SOSA, Ignacio ORONA CASTILLO y Cirilo VÁZQUEZ VÁZQUEZ
Universidad Juárez del Estado de Durango, Facultad
de Agricultura y Zootecnia, División de Estudios de Postgrado, Apartado Postal
142, CP 35000. Gómez Palacio, Durango, México. E-mail: jose_dimaslopez@hotmail.com
 Autor para correspondencia
Autor para correspondencia
|
Recibido:
22/09/2009 |
Fin
de arbitraje: 12/09/2010 |
Revisión recibida: 10/11/2010 |
Aceptado: 28/11/2010 |
RESUMEN
Con el objeto de seleccionar el mejor genotipo para las condiciones
agroecológicas de El Ejido Francisco Villa, municipio de Lerdo, Durango,
México, se evaluaron cuatro genotipos de maíz. La siembra se realizó el 23 de
agosto de 2007 en surcos separados a 0,8 m y a una distancia entre planta de
0,2 m, se fertilizó con 80 kg de N y 17,48 kg de P por hectárea. Se utilizaron
dos híbridos (H-412 y H419) y dos variedades de polinización libre, Blanco Hualahuises y San Lorenzo.
De cada genotipo se registró el rendimiento de grano y la humedad
acumulada en el suelo. Se realizó análisis de covarianza entre rendimiento de
grano y humedad del suelo para conocer la relación entre las dos variables;
análisis en bloques al azar para rendimiento y se generaron los contrastes ortoganales pertinentes entre los tratamientos. Se utilizó
el análisis de componentes principales para discriminar a los genotipos. La
relación entre el rendimiento de grano y la humedad del suelo fue no
significativa. El mejor genotipo por rendimiento fue San Lorenzo y por
adaptación Blanco Hualahuises.
Palabras clave: Maíz, híbridos,
variedades, humedad del suelo, rendimiento de grano.
ABSTRACT
In order to select the best genotype for the agroecological conditions of Ejido
Francisco Villa, Durango, Municipality of Lerdo,
Durango, México, four materials were evaluated. The sowing was carried out on
August 23, 2007, in furrows at 0.8 m and a distance between plants of 0.2 m; it
was fertilized with 80 kg N and 17.48 kg P per hectare. Two hybrids (H-412 and
H-419) and two open pollination varieties (Blanco Hualahuises
and San Lorenzo) were used. Grain yield and soil moisture were recorded for
each genotype. An analysis of covariance between grain yield and soil moisture
was carried out to know the relationship between those variables; an analysis
of variance according to the completely randomized block design for grain yield
and orthogonals contrasts were generated among
treatments. A principal component analysis was used to discriminate genotypes.
The relationship among grain yield and soil moisture was not significant. The
best genotype for grain yield was San Lorenzo and for adaptation Blanco Hualahuises.
Key
words: Corn,
hybrids, varieties, soil moisture, grain yield.
INTRODUCCIÓN
El
maíz (Zea mays
L.) es uno de los tres cereales (junto con el trigo y el arroz) más importantes
del mundo. Actualmente se produce en casi 100 millones de hectáreas en 125 países
en desarrollo y se encuentra entre los tres cultivos más sembrados en 75 de
esos países (FAO, 2010). Cada año la mayor parte de los países con producción
agrícola dedican el 37% de cada hectárea con maíz. Estados Unidos y China
aportan el 40 y 19% de la producción mundial, respectivamente (FIRA, 1998). En
México se cultivan anualmente 7,5 millones de hectáreas, de las cuales el 15%
se cultiva bajo riego y el resto (85%) bajo condiciones de secano.
La
Comarca Lagunera se localiza en la parte central de la porción norte de México.
Se encuentra ubicada entre los meridianos 102°03'09” y 104°46'12” de LO y los
paralelos 24°22'21” y 26°52'54” LN. Su altura media sobre el nivel del mar es
de 1139 m. Su topografía es en general plana y de pendientes suaves, que varían
de 0,2 a 1,0 m/km, generalmente hacia norte y noreste. La temperatura media
anual es de alrededor de 20 °C, alcanzando una temperatura máxima extrema de 42
°C en el verano y una temperatura mínima extrema de -7 °C durante el invierno.
Su clima es considerado de tipo árido caliente y desértico, su precipitación
media anual es de alrededor de 220 mm, presentándose el período principal de
lluvias durante el verano y el otoño (Miranda Wong, 2008).
En
la Comarca Lagunera, se siembran aproximadamente cada año 123 mil hectáreas, de
las cuales el 53% se siembran en la parte del estado de Durango y el resto en
el estado de Coahuila, del 53%, el 12% son de temporal y de éstas más del 50,5%
se siembran con maíz para grano, con un promedio de 800 kg ha-1 (SAGARPA,
2000).
Aún cuando la superficie que se
dedica a este cultivo es relativamente baja, ésta toma importancia dada la
densidad de población humana ubicada en el área rural, pues tan solo en el municipio de Lerdo, Durango representa más
del 30% y donde éste cultivo es una fuente importante de su ingreso. Por tal
razón, es justificable el enfoque de investigación tendiente a mejorar el
estatus de vida de la población.
Existen
dos formas en que se puede lograr aumentos en la producción de los cultivos.
Una es mejorando las prácticas de cultivo y, otra, a través del mejoramiento
genético. La selección del mejor genotipo es relevante cuando se quiere
explotar al máximo el medio ambiente, la forma tradicional, rápida y económica,
es a través de la introducción, prueba y posterior selección de materiales y/o
genotipos (Duvick, 1996).
La
respuesta de los genotipos depende o está en función de cómo interaccionen con
el ambiente (Vincent y Woolley,
1972). Un genotipo que tenga un comportamiento medio aceptable en una
diversidad de ambientes, se dice que interacciona poco con el ambiente ó que es estable. Se han desarrollado diversas metodologías
que permiten hacer una separación de los efectos genéticos y no-genéticos (Finlay y Wilkinson, 1963).
La
clave para aumentar la producción agrícola estriba en incrementar la eficiencia
en la utilización de los recursos y lograr un mejor entendimiento de la
interacción del genotipo-ambiente (Kang, 2000). La
manifestación genotípica de las plantas depende en gran parte del medio que la
rodea. La interacción entre estos dos factores hace difícil el logro y la
magnitud de los avances genéticos en la prueba y selección de materiales. La
interacción genotipo–ambiente (GA) se refiere al comportamiento diferencial de
variedades o genotipos en ambientes diferentes. En mejoramiento genético el
investigador se enfrenta al problema de la diversidad ambiental y a la
respuesta relativa diferencial que muestran los genotipos al ambiente (Kearsey y Pooni, 1996). La
selección de genotipos apropiados para un ambiente específico, puede efectuarse
con relativa facilidad, pero a medida que los ambientes se diversifican, la
variabilidad ambiental se incrementa y en consecuencia las plantas pueden no
mantenerse dentro del rango de altos rendimientos (Romagosa
y Fox, 1993; Cienfuegos, 2000).
La
evaluación de genotipos se realiza con el propósito de obtener información
acerca del rendimiento y otras características agronómicas, pero no dan
información sobre la adaptación en general. Diversos métodos y/o técnicas han
sido desarrollados para analizar la interacción GA; la estimación y partición
de componentes de varianza, (Sprague y Federer, 1951; Miller et al. 1959a;1962b), el uso de
la regresión lineal (Yates y Cochran, 1938; Finlay y Wilkinson, 1963; Rowe y Andrew, 1964; Eberhart y
Russell, 1966; Bucio y Hill, 1966; Knight, 1970; Tai, 1971; Shulka, 1972); y los métodos multivariados, donde Fisher y Makenzie (1923), hicieron los primeros intentos, treinta
años después Williams (1952) amplió el concepto y mostró que la sumas de
cuadrados (SC) para la interacción puede ser representada por la suma de los eingenvalores de una matriz y, si la SC`s
para cualquiera o ambos de los efectos principales fueran sumados a esa
interacción, el resultado se mantiene con una matriz diferente. En el caso de
interacción, combinando ambientes y repeticiones, el modelo de variación entre
y dentro genotipos es: Yij = m + di
+ wij , donde wij representa
toda la variación dentro de genotipos, incluyendo el error (Mandel,
1969). Hasta 1972 el uso de estos análisis fue limitado, por la dificultad que
representaba el cálculo de los eingenvalores, por la
falta de equipo de cómputo (Freeman, 1973).
La
existencia de computadoras más rápidas, de mayor capacidad y la existencia de
software han promovido el uso de los análisis multivariados para el análisis de
la interacción GA, conocidos como modelos biliniales
y/o multiplicativos. En mejoramiento genético, el mas
conocido es el AMMI, propuesto por Gauch (1978), que
utiliza una parte aditiva y otra multiplicativa, donde esta última estima el
efecto de la interacción a través de componentes principales (Cruz y Hernández,
1994; Van Eeuwijk et al. 2000; Crossa y Cornelius; 2000). La técnica de componentes
principales, permite conocer la dimensionalidad y la
clasificación de datos, siempre y cuando dichas variables estén
correlacionadas, originando la formación de nuevas variables lineales
(componentes) y el peso y/o importancia relativa de cada variable (Genotipos) Jhonson (1998).
Por
tal motivo, el estudio se realizó con el objeto de identificar al mejor
genotipo para las condiciones de El Ejido Francisco Villa, municipio de Lerdo,
Durango, México.
MATERIALES y
MÉTODOS
El
trabajo se realizó en el ejido Francisco
Villa, Municipio de Lerdo,
Durango, México, localizado a los 20º 40’ 00” Norte y 103º 21’ 00” Oeste
a 1110 msnm. Se utilizaron cuatro genotipos de maíz: Dos variedades de
polinización libre, Blanco Hualahuises (G2) y San
Lorenzo (G3), y dos híbridos, el H-412
(G1) y H-419 (G4). La siembra se realizó
en agosto 23 de 2007 en surcos a 0,8 m y a una distancia entre plantas de 0,2
m; se fertilizó al momento de la siembra con 80 kg de nitrógeno y 17,48 kg de
fósforo por hectárea.
Se
cuantificó el agua almacenada en el suelo para cada experimento y
posteriormente se cuantificó la lámina de agua consumida por parcela.
Al
final del ciclo se cosechó por separado cada parcela y se pesó el grano,
transformándose a kilogramos por hectárea. Para determinar el grado de
influencia de la humedad en el rendimiento, los datos de las variables
rendimiento (Y) y lamina de agua (X) se analizaron
por covarianza; asimismo se realizaron gráficos de dispersión para cada
genotipo para ambas variables.
Con
el propósito de conocer el mejor genotipo, se usó un diseño de bloques al azar
con datos no balanceados en las repeticiones donde cada genotipo fue un
tratamiento y se aplicaron las técnicas de contrastes ortogonales y componentes principales para clasificar el
comportamiento de los genotipos tal como lo sugieren Cruz y Hernández (1994);
Van Eeuwijk et
al. (2000)
y Crossa y Cornelius (2000). Además, se generó un gráfico de dispersión con los
valores característicos de los dos componentes principales.
RESULTADOS Y DISCUSIÓN
En
el Cuadro 1 se muestra la cantidad de agua almacenada en el suelo en cada
genotipo y la lámina de agua consumida por parcela y el rendimiento promedio de
granos.
|
Cuadro 1. Valores y estadísticos de rendimiento promedio
de grano (Y) y lámina de agua consumida por parcela (X) en cuatro genotipos
de maíz (Zea mays
L.) en el ejido Francisco Villa, Durango. México. 2007. |
||||||||
|
Observa-ciones |
H-412 |
Blanco
Hualahuises |
San
Lorenzo |
H-419 |
||||
|
X † |
Y ‡ |
X |
Y |
X |
Y |
X |
Y |
|
|
1 |
6,1 |
976 |
5,0 |
1200 |
6,4 |
3090 |
8,2 |
2120 |
|
2 |
6,2 |
928 |
7,0 |
1482 |
6,4 |
2440 |
8,8 |
2090 |
|
3 |
6,3 |
1236 |
7,5 |
1282 |
6,8 |
2400 |
8,8 |
2430 |
|
4 |
6,5 |
1024 |
7,5 |
1141 |
7,3 |
1080 |
8,8 |
1590 |
|
5 |
7,5 |
1464 |
9,7 |
1229 |
7,3 |
950 |
8,9 |
2250 |
|
6 |
7,9 |
988 |
9,8 |
1364 |
7,3 |
950 |
9,0 |
1830 |
|
7 |
8,0 |
1156 |
9,8 |
1291 |
7,5 |
1010 |
9,2 |
2310 |
|
8 |
8,3 |
935 |
9,8 |
1265 |
7,5 |
1870 |
9,3 |
2770 |
|
9 |
8,3 |
1454 |
10,0 |
1439 |
7,6 |
1030 |
9,3 |
2200 |
|
10 |
8,4 |
962 |
10,6 |
1459 |
7,6 |
1620 |
9,3 |
2040 |
|
11 |
8,5 |
1304 |
10,8 |
1232 |
7,8 |
2010 |
9,3 |
2010 |
|
12 |
8,5 |
1500 |
10,8 |
1190 |
8,1 |
3060 |
9,6 |
1920 |
|
13 |
9,0 |
1600 |
10,8 |
1095 |
8,7 |
2730 |
9,8 |
3130 |
|
14 |
9,3 |
1450 |
11,0 |
1248 |
8,7 |
2150 |
9,9 |
2150 |
|
15 |
9,5 |
1112 |
11,2 |
1124 |
8,8 |
1700 |
9,9 |
2050 |
|
16 |
10,1 |
1120 |
11,4 |
1098 |
9,0 |
3030 |
10,0 |
1490 |
|
17 |
10,1 |
1468 |
11,4 |
995 |
9,2 |
1500 |
10,0 |
1280 |
|
18 |
10,1 |
1204 |
11,4 |
1042 |
9,2 |
940 |
10,1 |
1440 |
|
19 |
10,5 |
1456 |
11,5 |
916 |
9,2 |
2270 |
10,3 |
1640 |
|
20 |
|
|
11,6 |
1039 |
9,6 |
2850 |
10,5 |
1370 |
|
21 |
|
|
|
|
9,7 |
2260 |
10,5 |
1200 |
|
22 |
|
|
|
|
9,7 |
850 |
10,6 |
1800 |
|
23 |
|
|
|
|
10,0 |
2520 |
10,8 |
1250 |
|
Promedio |
8,4 |
1228,3 |
9,9 |
1206,6 |
8,2 |
1926,5 |
9,6 |
1928,7 |
|
Rango |
4,5 |
672,0 |
6,6 |
566,0 |
3,6 |
2240,0 |
2,6 |
1930,0 |
|
DS |
1,4 |
226,6 |
1,8 |
155,2 |
1,1 |
774,9 |
0,7 |
488,5 |
|
† Lámina de agua (cm); ‡Rendimiento en kg ha-1. |
||||||||
Los resultados del análisis de covarianza indica que el rendimiento
variable dependiente (Y) no estuvo significativamente
influenciado por el contenido de humedad (Cuadro 2). Aun cuando en los parámetros estadísticos del
Cuadro 1 se advierte que el rango en lámina consumida por los genotipos oscila
de 2,6 cm para el genotipo H-419 a 6,6 cm para Blanco Hualahuises,
y lo mismo se observa para las respectivas desviaciones estándar (DE). No se
observa un paralelismo entre la magnitud de estos dos parámetros y el
rendimiento. La anterior tendencia puede deberse a lo reportado por Pierre et al. (1965) quienes consideran
que las plantas que crecen en ambientes secos son más eficientes en el uso del
agua y por ende sufren menos pérdidas en su rendimiento.
|
Cuadro 2. Análisis de covarianza entre rendimiento
(y) y lámina de agua consumida (x) por cuatro genotipos de maíz (Zea mays L.)
en el ejido Francisco Villa, Durango. México. 2007. |
||||||
|
Fuente de variación |
G.L. |
SC(YY) |
Y
Ajustada por X |
|||
|
GL |
SC |
CM |
Ft |
|||
|
Total |
84 |
30500877.95 |
|
|
|
|
|
Rep |
22 |
6303489.62 |
|
|
|
|
|
Trat |
3 |
590818.19 |
|
|
|
|
|
Error |
23606569.39 |
58 |
23086559,94 |
403216,60 |
|
|
|
Trat + Error |
61 |
24197388.33 |
61 |
24178512,91 |
|
|
|
Trat Ajustado |
|
|
3 |
791952,97 |
263984,32 |
0,65
ns |
|
Bx/y = - 59,42 |
Intercepto=
1670,22 ± 990,8 |
|
||||
|
ns= no diferencia significativa al 0,05. |
||||||
En
el análisis de componentes principales los tres primeros componentes explicaron
el 90% de la varianza acumulada en los datos. En conjunto el componente 1 y 2 explican
el 66%, por tal razón se pueden utilizar para hacer inferencias acerca del
comportamiento de los genotipos (Cuadro 3).
|
Cuadro
3. Valores característicos, porcentaje de varianza y varianza acumulada en
cuatro genotipos de maíz (Zea mays L.) en el ejido Francisco Villa, Durango.
México. 2007. |
||
|
Componente |
% de varianza |
Varianza acumulada |
|
1 |
39,49 |
39,49 |
|
2 |
27,26 |
66,75 |
|
3 |
23,45 |
90,20 |
|
4 |
9,80 |
100,00 |
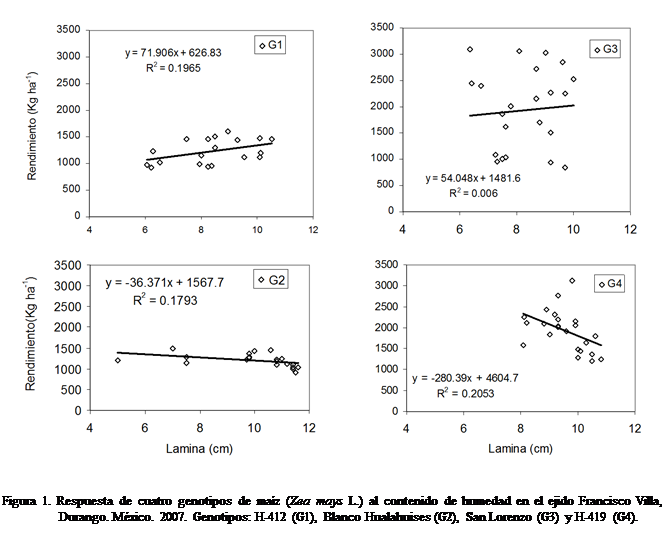
La dispersión de los datos de la Figura 1 para los cuatro genotipos
ratifica por la línea de tendencia la baja relación entre ambas variables por
la magnitud del coeficiente de determinación (R2). Las respuestas de
H-412 y Blanco Hualahuises son contrarias, pues en tanto H-412, muestra una respuesta positiva
con el incremento de humedad, Blanco Hualahuises responde negativamente. Algo similar ocurre
con Sam Lorenzo y H-419. Este comportamiento puede estar más relacionado con la
estabilidad ó adaptación a las condiciones del
ambiente de prueba, pues independientemente de la respuesta se observa menor
dispersión correlativamente en Blanco Hualahuises, H-412 y H-419 que en San Lorenzo. Los tres
primeros, al parecer son genotipos más uniformes genéticamente, en tanto San
Lorenzo es una variedad muy heterogénea lo que se refleja en la magnitud de la
desviación estándar (Cuadro 1). Blanco Hualahuises
con la menor DE (155,2) indica que es un genotipo de bajo rendimiento pero muy
adaptado a las condiciones típicas de las regiones áridas ó
que fue seleccionado para ó bajo esas condiciones. Lo
mismo puede decirse de H-412. Esta misma jerarquización se observa al realizar
los contrastes (Cuadro 4), pues H-412 y Blanco Hualahuises por la magnitud del rendimiento son estadísticamente
iguales entre sí y diferentes a San Lorenzo y H-419. Estos resultados coinciden con Vincent y Wolley (1972) quienes mencionan que las
deficiencias de humedad durante la formación y llenado de grano provocan una
disminución del número de grano por mazorca y/o peso de grano y por ende en
rendimiento dependiendo de la adaptación y estabilidad del genotipo y con Jurgens et al. (1978); Grant et
al. (1989) y Reta Sánchez y Martínez
(1990); quienes señalan que esta reducción de rendimiento es de 29 a 53%, al
reducir el peso medio del grano de 19 a 49%.
|
Cuadro 4. Análisis de varianza y contrastes
ortogonales de cuatro genotipos de maíz (Zea
mays L.) en
el ejido Francisco Villa, Durango. México. 2007. |
|||||
|
F.V. |
G.L. |
SC |
CM |
Fc |
Pr > F |
|
Modelo |
25 |
16205674,65 |
648226,98 |
2,68
|
0,0010 |
|
Trat |
3 |
11119788,95 |
3706596,31 |
15,30 |
0,0001
* |
|
Rep |
22 |
5547145,94 |
252142,99 |
1,04 |
0,4339 |
|
Error |
59 |
14295203,29 |
242291,58 |
|
|
|
Total
corregido |
84 |
30500877,95 |
|
|
|
|
R2
= 0,53 C. V. = 30,73% Promedio =1601,62 |
|||||
|
Contrastes |
G.L |
SC |
CM |
Fc |
Pr > F |
|
G1
vs G2 G3 G4 |
1 |
3353411,40 |
3353411,40 |
13,84 |
0,0004 |
|
G2
vs G3 G4 |
1 |
7766323,20 |
7766323,20 |
32,05 |
0,0001 |
|
G3
vs G4 |
1 |
54,34 |
54,34 |
0,00 |
0,9881 |
|
*
Diferencia significativa al 0,05. Genotipos:
H-412 (G1), Blanco Hualahuises (G2), San Lorenzo
(G3) y H-419 (G4) . |
|||||
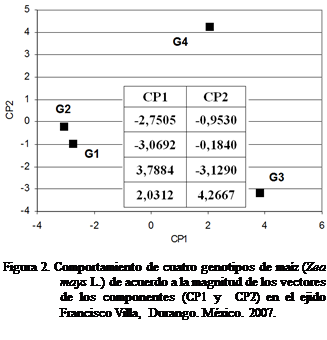
Con los
vectores de los dos primeros componentes se generó un gráfico de dispersión en
el cual se comprueba el comportamiento de los genotipos. De acuerdo a la
posición en la gráfica, los genotipos San Lorenzo y H-419 se ubican a la
derecha con respecto al eje “X” con valores de 3,78 y 2,03 unidades, que de
acuerdo a Cruz y Hernández (1994) son genotipos con rendimientos altos pero muy
variables en su respuesta con el ambiente y su lejanía del cero con respecto al
eje “Y” los clasifica como inconsistentes en su comportamiento promedio.
Lo
anterior se ratifica con la mayor dispersión de datos que se muestra en la
Figura 2. Los genotipos H-419 y Blanco Hualahuises,
se ubican en el lado negativo del eje “X” y muy cercanos al cero de “Y”, lo
cual los clasifica como genotipos de bajo rendimiento pero con mayor
estabilidad en su comportamiento medio. Lo anterior coincide con el
comportamiento de estos genotipos en la Figura 1.
CONCLUSIONES
Se
concluye que el rendimiento no estuvo influenciado por el agua acumulada en
cada muestreo. El mejor genotipo en este estudio con base a la variable
rendimiento fue la variedad San Lorenzo y con base a la estabilidad la variedad
Blanco Hualahuises. Además, el mejor genotipo no es
aquel que produce más, sino aquel que garantiza una producción más constante a
través del tiempo y/o en condiciones de siembra y manejo diferente.
LITERATURA CITADA
Bucio
A. L. and J. Hill. 1966. Environmental and genotype-environmental
components of variability. II. Heterozygote. Heredity, 21: 399-405.
Cienfuegos Rivas, E. G.
2000. Interacción genotipo-ambiente: Evaluación mediante la correlación
genética. In: Simposio Interacción genotipo x ambiente; Zavala y Treviño
editores. SOMEFI-CSSA-UG, del 15-20 de octubre, Irapuato México.
Crossa, J. and P. L.
Cornelius. 2000. Modelos lineales-bilineales para el análisis de ensayos de
genotipos en ambientes múltiples. In: Simposio Interacción genotipo x
ambiente; Zavala y Treviño editores. SOMEFI-CSSA-UG, del 15-20 de octubre,
Irapuato México.
Cruz, M. R. y A. Hernández. 1994. Análisis computacional de la
interacción genotipo-ambiente con el modelo AMMI. Revista Fitotecnia Mexicana. 17: 103-115.
Duvick, D. 1996. Plant breeding an
evolutionary concept. Crop Sci. 36: 539-548.
Eberhart,
S. A, and W. A. Russell. 1966. Stability
parameters for comparing varieties. Crop Sci. 6: 36-40.
Fideicomisos Instituidos en Relación con la
Agricultura (FIRA). 1998. Oportunidades de desarrollo del maíz mexicano,
alternativas de competitividad. Banco de México. Boletín informativo N0. 309
Volumen XXX, México p. 88.
Finlay, K. W, and G. N.
Wilkinson. 1963. The analysis of adaptation in a plant-breeding programme. Aust. J. Agric. Res. 14: 742-754.
Food and Agriculture
Organization (FAO). 2010. FAOSTAT. Disponible en:
http://faostat.fao.org/site/567/default.aspx. Consultado 25 de junio de 2010.
Fisher, R. A. and W. Aa Makenzie. 1923. Studios
in crop variation. II. The manorial response of different potato varieties. J.
Agric. Sci., 13: 311-320.
Freeman, G. H. 1973. Statistical methods for the
analysis of genotype-environment interactions. Heredity, 31: 339-354.
Guauch, H. G. 1978. Model selection
and validation for yield trials with interaction. Biometrics 44: 705-715.
Grant, R. F.; B. S. Jackson, J. R. Kiniry and G. F. Arkin. 1989. Water
deficit timing effects on yield components in maize. Agronomy J. 89:104-112.
Jurgens, S. K.; R. R. Johnson and J.
S, Boyer. 1978. Dry matter production and translocation in maize subjected to
drought during grain fill. Agronomy J. 70: 678-692.
Johnson, D. E. 1998.
Métodos multivariados aplicados al análisis de datos. Ed. International Thompson,
México.
Kang, M. S. 2000. Genotype-by-environment interaction
and performance stability in crop breeding. In : Simposio Interacción genotipo x ambiente; Zavala y Treviño editores. SOMEFI-CSSA-UG, del 15-20 de octubre, Irapuato México.
Kearsey,
M. J. and H. S. Pooni. 1996. The genetical
analysis of quantitative traits. Chapman and Hall, London,
UK.
Knight, R. 1970. The
measurement and interpretation of genotype - environmental interactions.
Euphytica, 19: 225-235.
Mandel, J. 1969. A method for
fitting empirical surfaces to physical or chemical data. Technometrics, 11: 411-429.
Miller, P. A.: J. C. Williams and H. F.
Robinson. 1959. Variety x environment interactions in cotton variety tests and
their implications on testing methods. Agron. J. 51: 132-134.
Miller, P. A.; H. F. Robinson
and O. A. Pope. 1962. Cotton variety testing: additional information
on variety x environment interactions. Crop Sci. 2: 349-352.
Miranda Wong, R. 2008. Caracterización de la
producción del cultivo de algodonero (Gossypium hirsutum L.) en la Comarca Lagunera. Revista Mexicana
de Agronegocios 23 (2):696-705
Pierre,
W. H.; D. Kirkham, J. Pesek
and R. Shaw. 1965. Plant environment and efficient
water use. American
Society of Agronomy. Madison,
Wisconsin, USA.
Reta-Sánchez, R, y M. A. Martínez. 1990. Influencia de diferentes
niveles de humedad en el suelo sobre el rendimiento de grano y producción de materia seca del maíz. ITEA 86V:37-45.
Romagosa,
I. and P. N. Fox. 1993. Genotype x environment interaction and
adaptation. p. 373-390. In: M. D.
Hayward, N. O. Bosemark and I. Romagosa
(Eds.). Plant breeding: Principles and prospects. Chapman and
Hall, New York, N.Y. USA.
Rowe, P. R, and R. A. Andrew. 1964. Phenotypic
stability for a systematic series of corn genotypes. Crop Sci. 4: 563-567.
Shulka, G. K. 1972. Some statistical aspects of partitioning genotype-enviromental components of variability. Heredity, 29: 237-245.
Secretaría de Agricultura, Ganadería,
Desarrollo Rural, Pesca y Alimentación (SAGARPA). 2000. Anuario Estadístico de
la Producción Agropecuaria 2000. Región Lagunera Coahuila-Durango, Alianza para
el Campo. Comité Estatal de Información Estadística y Geográfica del Sector Agroalimentario y
Pesquero.
Sprague, G. F. and W. T.
Federer. 1951. A comparison of
variance components in corn yield trials. II. Error, year x
variety, location x variety, and variety components. Agronomy J. 43: 535-541.
Tai, G. C. 1971. Genotypic stability
and its application in potato regional trials. Crop Science 11: 184-190.
Van Eeuwijk, F. A.;
J. Crossa, M. Vargas and J. M. Ribaut. 2000. Modeling QTLS
and QTL x E using factorial regression models and partial least squares techniques. In: García y Treviño (eds.). Simposium:
Interacción genotipo x ambiente. SOMEFI-CSSA-UG. Irapuato, Guanajuato,
México.
Vincent, G. B. and D. G. Woolley. 1972. Effect of
moisture stress at different stages of growth: II. Cytoplasmic
male-sterile corn. Agronomy J. 64: 599-602.
Williams, E. J. 1952. The
interpretation of interactions in factorial experiments. Biometrika, 39: 65-81.
Yates, F. and W. G. Cochran. 1938. The analysis
of group of experiments. J. Agric. Sci. 23: 556-580.
Página
diseñada por Prof. Jesús Rafael Méndez Natera
TABLA DE CONTENIDO DE LA REVISTA CIENTÍFICA UDO
AGRÍCOLA



