Descargar este artículo  en Formato PDF:

 

 

 

 

 

 

 

 

 

 

Revista Científica UDO Agrícola Volumen 10. Número 1. Año 2010. Páginas: 60-67

 

Dependencia espacial de algunas propiedades químicas superficiales del suelo y de algunas variables de producción en cultivos de crisantemo bajo invernadero

Spatial dependence of some superficial chemical properties of soil and of some variables of production in greenhouse cultivation of chrysanthemum

 

Daniel Francisco JARAMILLO JARAMILLO

 

Universidad Nacional de Colombia. Sede Medellín. Facultad de Ciencias, Escuela de Geociencias. Bloque 14 Oficina 215, Medellín, A.A. 3840. Colombia. E-mail: djaramal@unal.edu.co

 

 

RESUMEN

 

En un cultivo de crisantemo bajo invernadero, variedad Delistar, se estudió la dependencia espacial del pH y de la conductividad eléctrica superficiales del suelo, así como el diámetro de la flor y la altura y el peso de las plantas al momento de hacer la cosecha, mediante análisis de semivarianza. Se encontró una alta dependencia espacial de rango muy corto en todas las propiedades estudiadas. Los semivariogramas experimentales fueron predominantemente cíclicos y mostraron dos estructuras espaciales separadas por una distancia de 3 m, lo que se consideró como indicativo del efecto de los sistemas de preparación del terreno para establecer el cultivo y del manejo que se hace del mismo, donde muchas de las prácticas son manuales y pueden generar una alta heterogeneidad en las propiedades del suelo que se relacionan con las variables evaluadas que las distribuyen de forma casi anidada.

 

Palabras clave: Variabilidad espacial, semivarianza, pH del suelo, conductividad eléctrica del suelo, crisantemo, cultivo bajo invernadero.

 

ABSTRACT

 

In a commercial greenhouse cultivation of chrysanthemum Delistar variety, spatial dependence was studied by means of semivariance analysis of pH and superficial electric conductivity of soils, as well as flower diameter and height and weight of plants to the moment of harvest. There was high spatial dependence of very short range in all properties studied. Experimental semivariograms were dominated by cyclical forms and showed two spatial structures separated by a distance of 3 m, which were considered as indicative of the effect of crop management systems, where many practices are manual and can generate a high heterogeneity in the soil properties that relate to the evaluated variables that distributes almost nested.

 

Key words: Spatial variability, semivariance, soil pH, electric conductivity of soil, chrysanthemum, greenhouse cultivation.

 

 

INTRODUCCIÓN

 

Existe una gran variabilidad en las propiedades del suelo que depende de la propiedad que se considere, siendo más variables las propiedades químicas que las físicas y más en aquellos suelos que están siendo sometidos a uso que en los que están en su condición natural (Ovalles, 1992). El suelo puede variar espacialmente en sus propiedades debido a los procesos naturales que han actuado en su formación (Goovaerts, 1998, 1999; Briggs et al., 2006) y/o debido al manejo que se hace en él (Cambardella y Karlen, 1999; Paz-González et al., 2000; Jaramillo, 2008a; Jaramillo et al., 2008). Así mismo, la variabilidad depende de la escala de trabajo (Goovaerts, 1998, 1999; Amador et al., 2000; Facchinelli et al., 2001; Lin, 2002; Lin et al., 2006; Webster y Oliver, 2007; Gallardo y Maestre, 2008; Guastaferro et al., 2010).

 

El pH y la conductividad eléctrica se tienen como indicadores de calidad del suelo (Soil Quality Institute (SQI), 1999; Moral et al., 2010) e Infoagro (s.f.) informa que tanto se relacionan con la cantidad y la calidad de la producción de crisantemo. Lopera y López (1997), en cultivos de Aster bajo invernadero en el Oriente Antioqueño, observaron que en los primeros 0,15 m del suelo el 53,46 % de la variabilidad del pH se producía a distancias menores a 60 cm y que el 30,59 % de dicha variabilidad se presentaba a distancias mayores de 30 m. También encontraron que el 14,13 % de la variabilidad de la conductividad eléctrica se daba a menos de 0,60 m de distancia y que el 73,64 % se acumulaba a distancias mayores a 30 m.

 

Jaramillo (2010) estudió, mediante un diseño anidado en el que los factores fueron diferentes distancias de muestreo, la variabilidad espacial de la temperatura del suelo medida a 0,10 m de profundidad y tres propiedades de calidad de las flores de crisantemo cultivadas bajo invernadero: peso del tallo, diámetro de la flor y altura de la planta, encontrando que la mayor parte de la variabilidad en todas las variables se acumuló en distancias menores a 0,80 m.

 

Con el presente trabajo se estudió la dependencia espacial del pH y la conductividad eléctrica del suelo medidas a 0,10 m de profundidad, así como la estructura espacial de tres propiedades de calidad de las flores de crisantemo cultivadas bajo invernadero: peso del tallo, diámetro de la flor y altura de la planta.

 

MATERIALES Y MÉTODOS

 

El estudio se realizó en un cultivo de flores bajo condiciones de invernadero, ubicado en el sector de Llano Grande, Oriente Antioqueño, con coordenadas 6° 8’ 31’’ N, 75° 25’ 15’’ W. Se trabajó con flores de crisantemo, variedad Delistar, sembradas en camas de 30 m de largo por 1,20 m de ancho, con un espacio entre camas de 0,40 m para tráfico, lo que permitió tener alrededor de 192 camas ha^-1. El cultivo tenía seis años cuando fue muestreado.

 

Los suelos en que se desarrolló el cultivo, según resultados de análisis de laboratorio hechos el 2 de mayo de 2007, fueron de reacción neutra (pH de 6,8), con una conductividad eléctrica de 0,6 dS m^-1, texturas medias (franco limosas) y densidad aparente baja (0,69 Mg m^-3); presentaron contenidos relativamente altos de P, K, Ca, Mg, NO₃^-, S, Fe, Mn, Zn y B, con valores de 78, 324, 3739, 512, 300, 100, 223, 33, 2,2 y 0,93 ppm, respectivamente; sólo el Cu se encontró en cantidades relativamente bajas (0,6 ppm).

 

Las variables evaluadas fueron:

 

·         pH: Se midió el pH del suelo superficial tomando una muestra del mismo y haciendo una suspensión de ella en agua en una proporción volumétrica 1:1. Al cabo de media hora de haber hecho la suspensión, agitándola esporádicamente, se hizo la lectura del pH con un pHmetro digital de campo (pHTestr®) y con una precisión instrumental de 0,1 unidades de pH.

 

·         CE: Conductividad eléctrica medida en la misma suspensión en que se midió el pH con un conductivímetro digital de campo (ECTestr®) y con una precisión instrumental de 0,1 dS m^-1.

 

·         P: Peso del tallo con la flor, cortado en el cuello de la planta, medido con una balanza colgante de resorte y precisión instrumental de 0,1 g.

 

·         D: Diámetro de la flor medido con una regla y precisión instrumental de 1 mm.

 

·         A: Altura de la planta desde la superficie del suelo hasta el plano superior de la flor, medida con flexómetro y precisión instrumental de 1 mm.

 

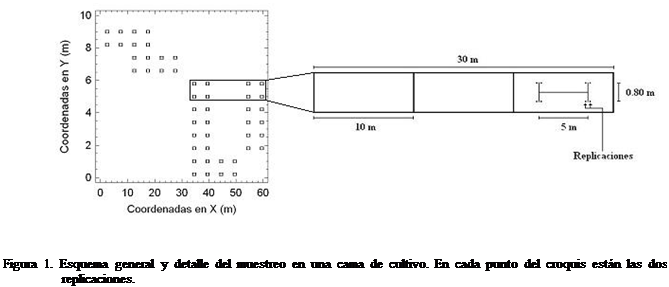
El muestreo se hizo en 6 camas de 30 m de largo, seleccionadas al azar dentro de una nave de cultivo compuesta por 12 camas. Cada cama se dividió en 3 porciones iguales de 10 m de las que se seleccionaron, también al azar, dos. En la parte central de cada porción de cama seleccionada anteriormente se delimitó un eje de 5 m de longitud y en cada uno de los extremos de este eje se ubicaron líneas perpendiculares a él y centradas, de 0,80 m de longitud. En los extremos de la última línea se hicieron dos determinaciones separadas 0,20 m. Se tuvo así un total de 6 x 2 x 2 x 2 x 2 = 96 muestras. Los sitios muestreados fueron georreferenciados en un plano de coordenadas cartesianas cuyo origen fue tomado arbitrariamente (Figura 1).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

El análisis de semivarianza exige cumplir los supuestos de normalidad en la distribución de los datos y de estacionaridad de varianza y media en ellos (Goovaerts, 1998, 1999; Gringarten y Deutsch, 2001; Webster y Oliver, 2007). Se confirmó el supuesto de normalidad en los datos con el estadístico de Shapiro-Wilk: si el valor p del estadístico era mayor a 0,05, los datos procedían de una distribución normal. Si la distribución no fue normal se evaluó la simetría de los datos: si fueron simétricos se suplió la falta de normalidad con esta característica (Jaramillo, 2005, 2006, 2008a, 2008b, 2009; Jaramillo et al., 2008).

 

Luego se confirmó el supuesto de estacionaridad para establecer si había o no alguna tendencia espacial en los datos. La confirmación de este supuesto se hizo mediante una regresión múltiple donde la variable en estudio fue la variable dependiente y las coordenadas de los puntos de muestreo las independientes. Si con este análisis se obtiene un modelo estadísticamente significativo, el análisis de semivarianza se hace con los residuales del mismo (Pradere, 1999; Bocchi et al., 2000; Schabenberger y Pierce, 2002; Diggle y Ribeiro, 2007; Gallardo y Maestre, 2008; Castañeda et al., 2010; Moral et al., 2010). El modelo estadístico para hacer este análisis fue del estilo (Jaramillo, 2008a, 2008b, 2009):

 

 

Donde x, y son las coordenadas.

 

En caso de que no se cumpliera alguno de los supuestos se hicieron transformaciones sencillas (logarítmica, inversa o raíz cuadrada) de los datos para normalizarlos o, por lo menos, volverlos simétricos. Finalmente se definió con cuales datos se haría el análisis de semivarianza: originales, transformados o residuales de la regresión. Se hizo un análisis descriptivo de los datos seleccionados con el fin de conocer sus principales propiedades estadísticas y luego se procedió a llevar a cabo los análisis de semivarianza correspondientes. Todos los análisis estadísticos se hicieron con los programas Statgraphics 5,1 plus y GS⁺ 9.0.

RESULTADOS Y DISCUSIÓN

 

Después de realizar los análisis descriptivos de las variables con sus datos originales se vio la necesidad de transformar la CE y el peso de la planta para normalizar su distribución. Con la transformación logarítmica se logró este cometido y en el Cuadro 1 se presentan los principales estadísticos que caracterizan las propiedades evaluadas. Se presentó una alta variabilidad en el log CE con respecto a las demás variables, y todas fueron simétricas en su distribución. Se presentaron correlaciones significativas al 95 % entre el pH y el diámetro de la flor, al 99 % entre el pH y la altura de la planta y al 99,9 % entre el peso de la planta con su altura y con el diámetro de su flor.

 

 

Cuadro 1. Principales estadísticos* de las variables** estudiadas en un cultivo de crisantemo bajo invernadero en el Oriente Antioqueño (Colombia) (n = 96).
Estadísticos	pH	log CE (dS m-1)	log Peso de planta (g)	Altura de planta (cm)	Diámetro de flor (cm)
Promedio	6,0	-0,46	1,751	108,51	14,99
Desviación estándar	0,18	0,22	0,1035	7,3025	1,8162
C.V. (%)	2,97	46,92	5,91	6,73	12,12
Mínimo	5,6	-1,0	1,4771	91,0	9,7
Máximo	6,4	-0,0458	2,0792	126,0	19,0
Asimetría	-0,2646	-1,7194	0,6849	-0,2066	0,9473
Kurtosis	-0,9644	0,3723	1,2386	-0,9157	0,5542
*   C.V.: Coeficiente de Variación. ** log: Logaritmo base 10. CE: Conductividad eléctrica.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Los análisis de tendencia espacial dieron los resultados que se presentan en el Cuadro 2. De acuerdo con estos resultados todas las propiedades presentaron tendencia espacial, aunque ésta sólo fue relevante, según criterio de Kerry y Oliver (2004) y de Jaramillo (2008b), en el diámetro de la flor ya que presentó un coeficiente de determinación R² > 20 %. Con base en lo encontrado en los análisis anteriores se determinó que las variables para hacer el análisis de semivarianza fueran los valores originales del pH (pH) y de la altura de la planta (A), los datos transformados a logaritmo de la CE (logCE) y del peso de la planta (logP), y los residuales de la tendencia del diámetro de la flor (restendD).

 

 

 

Cuadro 2. Resultados del análisis de tendencia espacial de pH y conductividad eléctrica (logCE) del suelo, del peso (logP) y altura de la planta (A), y del diámetro de la flor (D) de crisantemo bajo invernadero en el Oriente Antioqueño (Colombia).
Modelo	Valor p modelo	R2 (%)
pH = 6,07346 - 0,0155157*y	0,0177	4,84
logCE = -0,241575 - 0,00621182*x + 0,0703038*y - 0,01132*y2	0,0163	7,6
logP = 1,80501- 0,0117515*y	0,0018	8,98
A = 97,3702 + 0,140275*x + 7,52814*y - 0,0677025*x*y - 0,680476*y2	0,0060	10,79
D = 17,7697 - 0,0625717*x - 0,619033*y + 0,0174253*x*y	0,0000	22,79

 

 

 

 

 

 

 

 

 

 

 

 

 

 

El análisis de semivarianza arrojó los resultados que se muestran en el Cuadro 3 y la Figura 2. Se analizaron varios semivariogramas utilizando diferentes combinaciones de alcance y lag y se encontró que los semivariogramas más estables se presentaron cuando se utilizó un alcance de 6,4 m y un lag de 0,80 m. Con estas condiciones el número mínimo de pares comparados para establecer la semivarianza fue de 76 en el primer lag, cantidad suficiente para que la estimación de aquella sea confiable, según las recomendaciones de varios autores como Hamlett et al. (1986), McBratney y Webster (1986), Ovalles (1992), Dhillon et al. (1994) y Webster y Oliver (2007).

 

 

 

Cuadro 3. Estructura de la dependencia espacial del pH y la conductividad eléctrica (logCE) del suelo, del peso (logP) y altura (A) de las plantas, y del diámetro de las flores (restendD) de crisantemo bajo invernadero en el Oriente Antioqueño (Colombia).
Variable	Modelo	Nugget	Sill	Rango (m)	C/Sill (%)*	R2 (%)
pH	Exponencial	0,0006	0,0285	0,96	97,9	64,6
logCE	Esférico	0,0039	0,0493	0,95	92,1	34,8
logP	Esférico	1E-5	0,0089	0,81	99,9	16,2
A	Esférico	7,6	67,03	2,00	88,7	60,4
restendD	Esférico	2210	21430	0,70	89,7	10,1
* Porcentaje de la variabilidad total (Sill) que corresponde a variabilidad estructurada (C = Sill - Nugget).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

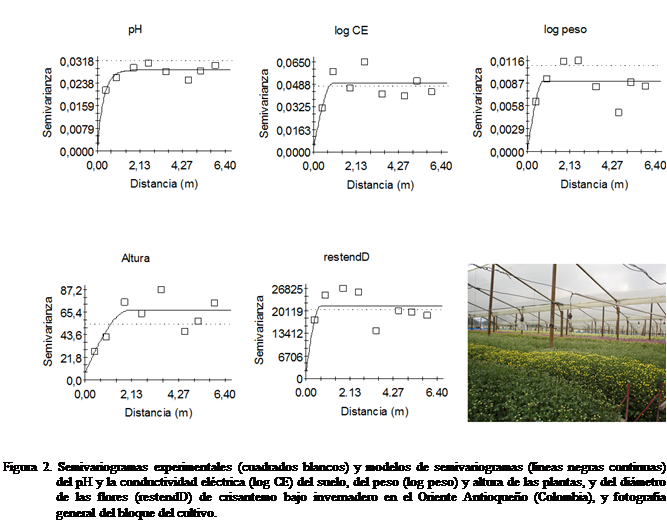
El análisis de semivarianza muestra que todas las variables presentaron dependencia espacial y que ésta fue alta, según los criterios de Cambardella et al., (1994), ya que tienen un valor de C/Sill mayor al 75% y un valor de nugget bajo. Además, dicha dependencia espacial fue de rango muy corto: 1,084 m en promedio, aunque cuatro de las cinco propiedades tuvieron rango menor a 1 m. Estos resultados ratifican lo que encontró Jaramillo (2010) al estudiar la variabilidad espacial de las variables relacionadas con la calidad de la producción en el mismo cultivo, mediante un diseño experimental anidado cuyos factores fueron distancias entre muestras. En dicho trabajo el autor encontró que más del 50 % de la varianza se acumuló a distancias de muestreo menores a 0,80 m, concluyendo que o tenían un alto componente aleatorio en la variabilidad total de las mismas o tenían una alta dependencia espacial de rango muy corto. Con este trabajo se confirmó la segunda opción.

 

En los semivariogramas experimentales de la Figura 2 se aprecia una forma general casi cíclica: hay una estructura espacial que muestra una acumulación de semivarianza al aumentar la distancia hasta alrededor de los 2 m, que luego desciende hasta cerca de los 4,25 m para volver a iniciar otro ciclo de acumulación. Webster y Oliver (2007) y Krasilnikov (2008) comprobaron que este comportamiento es ocasionado por la presencia de alguna tendencia cuadrática en los datos que, según Diggle y Ribeiro (2007), no necesariamente es espacial sino que puede estar controlada por algún atributo del suelo o externo a él. En la fotografía insertada en la Figura 2 puede verse claramente que, por lo menos en la altura de las plantas hay dicha tendencia.

 

Con las variables que presentaron correlación significativa se hicieron semivariogramas cruzados con el fin de estudiar su variabilidad conjunta (Cuadro 4 y Figura 3), los cuales se estimaron con la ecuación presentada por Goovaerts (1998) y por Webster y Oliver (2007):

 

                     

Donde:

 

     z, y son las dos variables continuas.

     h: Distancia entre puntos de muestreo (lag).

     N: Número de pares comparados para establecer la semivarianza (γ) en un determinado lag.

     z(u_α), z(u_α+h), y(u_α) o y(u_α+h): Valor de la variable z o y en la posición (u_α) o (u_α+h).

 

 

 

Cuadro 4. Parámetros de los semivariogramas cruzados entre pH - altura de la planta (pH x A), pH -  diámetro de la flor (pH x restendD), peso de la planta - diámetro de la flor (logP x restendD) y peso de la planta - altura de la planta (logP x A).
Variables	Modelo	Nugget	Sill	Rango (m)	C/Sill (%)*	R2 (%)
pH x A	Esférico	-0,001	-0,493	2,44	99,8	75,0
pH x restendD	Nugget	-0,566	-0,566	-	0,0	-
logP x restendD	Nugget	4,859	4,859	-	0,0	-
logP x A	Esférico	0,0436	0,3022	1,66	85,6	21,2
* Porcentaje de la variabilidad total (Sill) que corresponde a variabilidad estructurada (C).

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

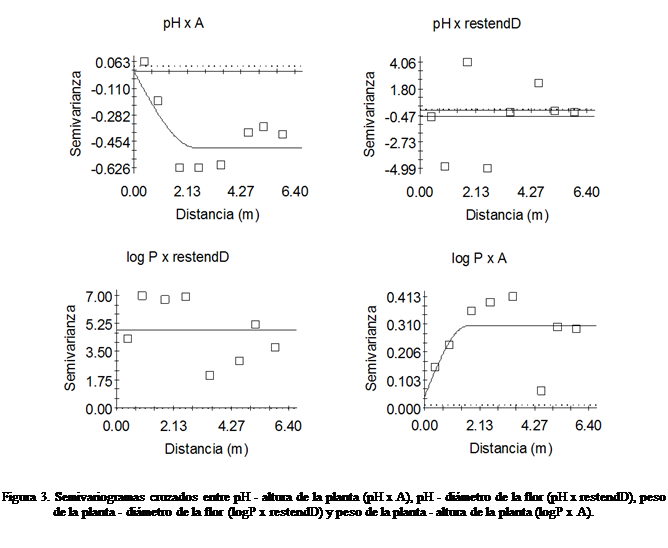
     Los semivariogramas cruzados de pH x restendD y log P x restendD fueron de nugget puro lo que implica que a pesar de que cada una de las variables por separado tiene dependencia espacial y están correlacionadas, cuando se analizan conjuntamente no presentan correlación espacial. Este comportamiento confirma que la correlación significativa entre el pH y el peso de la planta, con el diámetro de la flor, tiene un componente de tendencia espacial ya que al ser retirado este componente y trabajar con los residuales de la tendencia, la correlación espacial entre ellas desaparece. En todos los variogramas experimentales de las Figuras 2 y 3 se aprecia un cambio en la estructura espacial ubicado alrededor de los 3 m de distancia, siendo más notorio en el semivariograma simple de A (Figura 2) y en los cruzados (log P x restendD) y (log P x A) de la Figura 3, lo que sugiere la presencia de dos estructuras espaciales actuando a diferente escala, las cuales podrían estar controladas por las actividades de manejo del cultivo, muy manuales y por tanto difíciles de hacer en forma homogénea, sobre todo teniendo en cuenta el sistema de siembra del cultivo en camas que puede generar diferencias al interior de las mismas por el efecto de borde. Llama la atención que no se presente modelo de dependencia espacial en los semivariogramas cruzados que involucran el diámetro de la flor puesto que el variograma simple de este atributo sí lo presentó.

 

CONCLUSIONES

 

En todas las propiedades evaluadas en los suelos y cultivo estudiados se presentó una alta dependencia espacial de rango muy corto. Tanto en los variogramas experimentales simples, como en los cruzados de las variables que tuvieron correlación significativa, se detectó la presencia de dos estructuras espaciales separadas aproximadamente 3 m que sugieren dependencia espacial en dos escalas diferentes.

 

El comportamiento observado en los semivariogramas experimentales se ha interpretado como indicativo de que los sistemas de preparación del terreno para establecer el cultivo y del manejo que se hace de los mismos, donde muchas de las prácticas son manuales, pueden generar una alta heterogeneidad en las propiedades del suelo que se relacionan con las variables evaluadas, las que se pueden distribuir de manera casi anidada por efecto del diseño de la siembra y del tamaño de las unidades de producción que pueden generar efectos importantes de borde.

 

Es recomendable ampliar el presente estudio haciendo un muestreo más intenso y con una cobertura más completa del área para tratar de establecer las condiciones que están favoreciendo los comportamientos observados en el mismo.

 

LITERATURA CITADA

 

Amador, J. A.; Y. Wang; M. C. Savin and J. H. Görres. 2000. Fine-scale spatial variability of physical and biological soil properties in Kingston, Rode Island. Geoderma 98: 83-94.

 

Bocchi, S.; Castrignanò, A.; Fornaro, F.; Maggiore, T. 2000. Application of factorial kriging for mapping soil variation at field scale. European Journal of Agronomy 13: 295-308.

 

Briggs, C. A. D.; A. J. Busacca and P. A. McDaniel. 2006. Pedogenic processes and soil-landscape relationships in North Cascades National Park, Washington. Geoderma 137: 192-204.

 

Cambardella, C. A. y Karlen, D. 1999. Spatial analysis of soil fertility parameters. Precision Agriculture 1: 5-14.

 

Cambardella, C., T. B. Moorman, J. M. Novak, T. B. Parkin, D. L. Karlen, R. F Turco and A. E, Konopka. 1994. Field-scale variability of soil properties in Central Iowa soils. Soil Science Society American Journal 58: 1501-1511.

 

Castañeda, D. A.; Jaramillo, D. F.; Cotes, J. M. 2010. Componentes de la variabilidad espacial en el manejo por sitio específico en banano. Pesquisa Agropecuária Brasileira 45: 836-845.

 

Dhillon, N. S.; J. S. Samra; U. S. Sadana y D. R. Nielsen. 1994. Spatial variability of soil test values in a Typic Ustochrept. Soil Technology 7: 163-171.

 

Diggle, P. J.; Ribeiro Junior, P. J. 2007. Model-based Geostatistics. New York: Springer. 212 p.

 

Facchinelli, A.; Sacchi, E.; Mallen, L. 2001. Multivariate statistical and GIS-based approach to identify heavy metal sources in soils. Environmental Pollution 114: 313-324.

 

Gallardo, A.; Maestre, F. T. 2008. Métodos geoestadísticos para el análisis de datos ecológicos espacialmente explícitos. In: F. T. Maestre, A. Escudero y A. Bonet. (Ed.). Introducción al análisis especial de datos en ecología y ciencias ambientales: Métodos y aplicaciones. Universidad Rey Juan Carlos. Editorial Dykinson S.L. Madrid. p. 215-272.

 

Goovaerts, P. 1998. Geostatistical tolos for characterizing the spatial variability of microbiological and physico-chemical soil properties. Biol. Fertil. Soils 27: 315-334.

 

Goovaerts, P. 1999. Geostatistics in soil science: state-of-art and perspectives. Geoderma 89: 1-45.

 

Gringarten, E. and C. V. Deutsch. 2001. Teacher’s Aide Variogram Interpretation and Modeling. Mathematical Geology 33 (4): 507-534.

 

Guastaferro, F.; Castrignanò, A.; De Benedetto, D.; Sollitto, D.; Troccoli, A.; Cafarelli, B. 2010. A comparison of different algorithms for the delineation of management zones. Precision Agriculture 11: 600-620.

 

Hamlett, J. M.; R. Horton y N. A. C. Cressie. 1986. Resistant and exploratory techniques for use in semivariograms analysis. Soil Science Society American Journal 50: 868-875.

 

Infoagro. s.f.. El cultivo de la gérbera. [En línea]. (s. n.). [Consultado el 11 de septiembre de 2007]. Disponible en http://www.infoagro.com.

 

Jaramillo, D. F. 2005. Efecto de la variabilidad sistemática en experimentos de fertilización con fríjol: Primera siembra. Revista Facultad Nacional de Agronomía Medellín 58(1): 2717-2732.

 

Jaramillo, D. F. 2006. Efecto de la variabilidad sistemática en experimentos de fertilización con fríjol: Segunda siembra. Revista Facultad Nacional de Agronomía Medellín 59(1): 3147-3165.

 

Jaramillo, D. F. 2008a. Variabilidad espacial de las propiedades químicas del epipedón de un Andisol hidromórfico del Oriente Antioqueño (Colombia). Revista Facultad Nacional de Agronomía Medellín 61(2): 4588-4599.

 

Jaramillo, D. F. 2008b. Variabilidad espacial de rango largo de algunas propiedades químicas de Andisoles repelentes al agua de Antioquia. Suelos Ecuatoriales 38(1): 60-74.

 

Jaramillo, D. F. 2009. Variabilidad espacial de las propiedades ándicas de un Andisol hidromórfico del Oriente Antioqueño (Colombia). Revista Facultad Nacional de Agronomía Medellín 62(1): 4907-4921.

 

Jaramillo, D. F. 2010. Variabilidad espacial de la temperatura superficial del suelo y de algunas variables de producción en cultivos de crisantemo bajo invernadero. Revista Científica UDO Agrícola 10 (1): 68-75.

 

Jaramillo, D. F.; H. González y F. Álvarez. 2008. Variabilidad espacial de algunas propiedades físico-mecánicas de suelos de textura pesada. Revista CES Medicina Veterinaria y Zootecnia 3(2): 10-19.

 

Kerry, R. y M. A. Oliver. 2004. Average variograms to guide soil sampling. International Journal of Applied Earth Observation and Geoinformation 5: 307-325.

 

Krasilnikov, P. 2008. Chapter 2. Variography of discrete soil properties. In: Soil geography and geostatistics European Communities. Krasilnikov, P.; F. Carré and L. Montanarella eds. Luxembourg. pp: 12-25.

 

Lin, Y. B.; Lin, Y. P.; Liu, CH. W.; Tan, Y. CH. 2006. Mapping of spatial multi.scale sources of arsenic variation in groundwater on ChiaNan floodplain of Taiwan. Science of the Total Environment 370: 168-181.

 

Lin, Y. P. 2002. Multivariate geostatistical methods to identify and map spatial variations of soil heavy metals. Environmental Goeology 42: 1-10.

 

Lopera, M. y L. C. López. 1997. Variabilidad espacial de la salinidad en suelos con cultivo de flores bajo invernadero. Trabajo de Grado Ingeniero Agrónomo. Facultad de Ciencias Agropecuarias. Universidad Nacional de Colombia. Medellín. 66 p.

 

McBratney, A. B. y R. Webster. 1986. Choosing functions for semi-variograms of soil properties and fitting them to sampling estimates. Journal of Soil Science 37: 617-639.

 

Moral, F. J.; Terrón, J. M.; Marques Da Silva, J. R. 2010. Delineation of management zones using mobile measurements of soil apparent electrical conductivity and multivariate geostatistical techniques. Soil & Tillage Research 106: 335-343.

 

Ovalles, F. 1992. Metodología para determinar la superficie representada por muestras tomadas con fines de fertilidad. Serie B. FONAIAP-CENIAP-IIAG. Maracay. 44 p.

 

Paz González, A., Vieira, S. R. and Taboada, M. 2000. The effect of cultivation on the spatial variability of selected properties of an umbric horizon. Geoderma 97: 273-292.

 

Pradere, R. 1999. Definición de patrones homogéneos de pluviosidad en los Llanos Centrales venezolanos mediante kriging factorial. Agronomía Tropical 49(3): 297-325.

 

Schabenberger, O.; Pierce, F.J. 2002. Contemporary statistical models for the plant and soil sciences. New York: CRC Press. 738 p.

 

Soil Quality Institute (SQI). 1999. Soil Quality Test Kit Guide. USDA. U.S.A. 82 p.

 

Webster, R. and M. Oliver. 2007. Geostatistics for environmental scientists. 2nd ed. John Wiley and Sons, Ltd. England. 315 p.

 

 

Página diseñada por Prof. Jesús Rafael Méndez Natera

 

 

 

 

TABLA DE CONTENIDO DE LA REVISTA CIENTÍFICA UDO AGRÍCOLA

 

		Descargar este artículo  en Formato PDF:
			Obtenga el Lector de Archivos PDF